2023. 3. 16. 13:57ㆍAlgorithm
이번 글에서는 알고리즘 분석(=실행 시간 및 메모리 사용량 예측)에 대해 살펴볼 것이다.
알고리즘 분석을 하는 대표적인 이유는 "알고리즘 성능을 예측하여, 클라이언트에게 확신을 주기 위함"이다.
"Scienific method"을 사용해 알고리즘을 분석할 것이다.
Scienitic method
- Observe: 프로그램 실행 시간(=event)의 특징(=feature)을 관찰한다. (computer = natural world)
- Hypothesize: 실행 시간(=data)과 일치하는(or 비슷한) 가설을 설계(=modeling)한다.
- Predict: 가설을 사용해, (입력값이 다른) 프로그램 실행 시간(=another event)을 예측한다.
- Verify: 더 많은 events을 예측해본다.
- Validate: 예측 값(=prediction)과 실제 값(=answer)이 일치할 때까지 2 ~ 4번을 반복한다.
1. Empirical models
Empirical model은 실행 시간 비율(=ratio)로 가설을 설계(=modeling)한다.
1.1. Example: 3-sum problem
// 3-SUM problem: Given N distinct integers, how many triples sum to exactly zero?
public static int count(int[] a)
{
int N = a.length;
int count = 0;
for (int = 0; i < N; i++)
for (int j = i+1; j < N; j++)
for (int k = j+1; k < N; k++)
if (a[i] + a[j] + a[k] == 0)
count++;
return count;
}1.2. Observation
| N(size of problem) | time(seconds) |
| 250 | 0.0 |
| 500 | 0.0 |
| 1,000 | 0.1 |
| 2,000 | 0.8 |
| 4,000 | 6.4 |
| 8,000 | 51.1 |
| 16,000 | ? |
1.3. Hypothesis
실행시간과 입력 크기의 관계를 그래프로 나타내 실행 시간 모델을 설계한다.
대부분의 알고리즘이 power law(=$aN^b$)을 따르기에, $\lg-\lg$ 그래프를 사용한다.
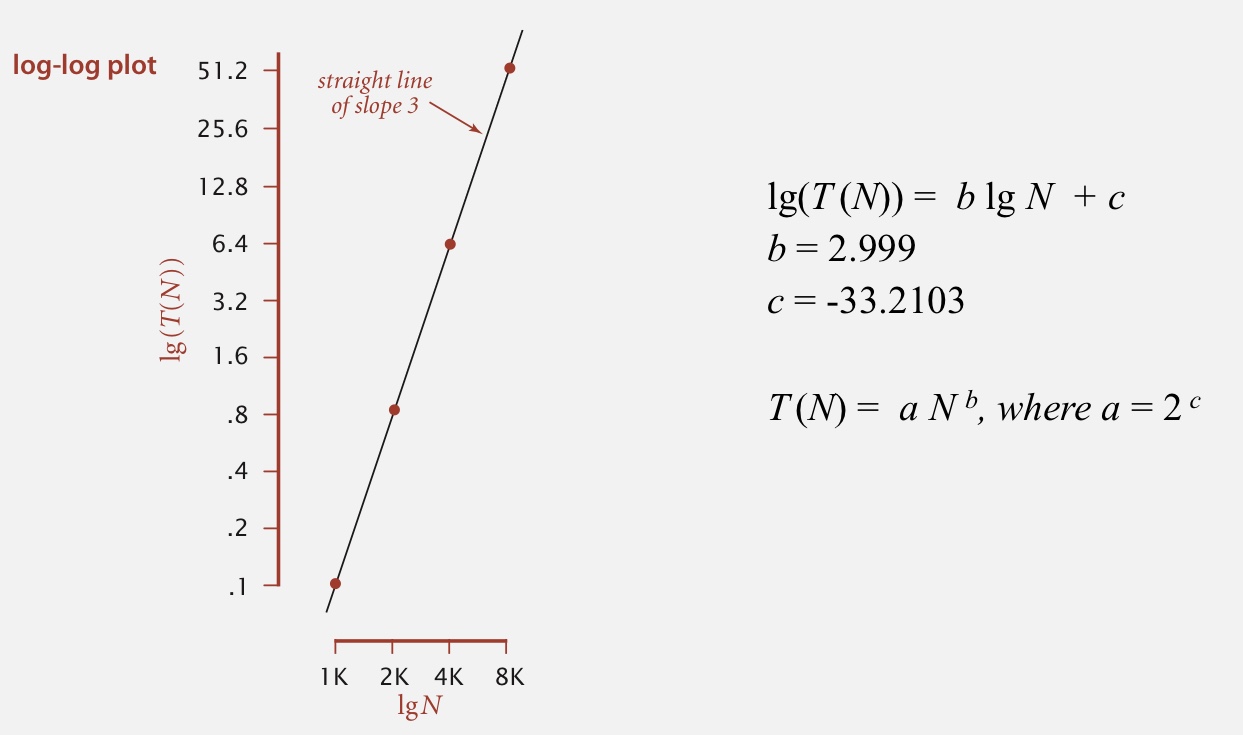
위 그래프를 기반으로, 실행 시간 모델을 다음과 같이 정의할 수 있다.
$$1.006 \times 2^{-10} \times N^{2.999} seconds$$
Doubling hypothesis
점진적으로, 문제 크기(=입력값 크기)를 두 배 증가시킨다.
그 다음, $\lg$ ratio를 계산해 $b$를 빠르게 구한다.
| N(size of problem) | time(seconds) | ratio | $\lg$ ratio |
| 250 | 0.0 | ||
| 500 | 0.0 | 4.8 | 2.3 |
| 1,000 | 0.1 | 6.9 | 2.8 |
| 2,000 | 0.8 | 7.7 | 2.9 |
| 4,000 | 6.4 | 8.0 | 3.0 |
| 8,000 | 51.1 | 8.0 | 3.0 |
| 16,000 | ? | ? | ? |
위 표에 기반해, $b = 3$로 추정할 수 있다.
$$\text{ratio}: \frac{a(2N)^b}{aN^b} = 2^b \rightarrow \text{lg ratio}: \lg 2^b = 3$$
위 event들 중 하나를 $\text{times} = aN^3$식에 대입하면, $a$를 쉽게 추정할 수 있다.
$$51.1 = a \times 8000^3 \rightarrow a = 0.998 \times 10^{-10}$$
Factor of running time
System independent factors (which effect $b$)
- Algorithm
- Input data
System dependent factors (which effect $a$)
- Hardware: CPU, Memory, cache, ...
- Software: compiler, iinterpreter, ...
- System: operating system, network, ...
2. Mathematical models
1). 연산의 빈도수와 2). 연산의 비용으로 수학적 모델(=가설)을 설계(=modeling)할 것이다.
이는 이전과 달리, 알고리즘의 동작 원리를 이해하는데 매우 큰 도움이 된다.
2.1. Specifying the calculation (by Donald Kruth)
$$\text{running time} = \vec{V}_\text{freq_of_all_oper} \times \vec{W}_\text{cost_of_all_oper}$$
위 수식을 사용하면, 알고리즘 실행 시간을 정확히 예측할 수 있다.
하지만 알고리즘이 복잡해질수록, 각 연산의 빈도수 계산이 매우 복잡해지는 단점이 있다.
2.2. Simplifying the calculations (by Alan Turing)
이 방법은 위 수학적 모델을 2단계 단순화하여, 설계(=modeling)하기 쉽다.
Simplification 1: basis operation
특정 연산(e.g., 1. 비용이 비싼 연산, 2. 빈도수가 높은 연산)만 이용해 수학적 모델을 만든다.
$$\text{running time} = \vec{V}_\text{freq_of_basis_oper} \times \vec{W}_\text{cost_of_basis_oper}$$
Simplification 2: tile notation
최대 차수를 제외한 나머지 차수를 무시한다. (e.g., $2N^2 + 20N + 1 \rightarrow \ \sim 2N^2$)
입력값 크기가 작을 때 어느 정도 오차가 발생하지만, 크기가 클 때는 무시해도 될 정도의 오차다.
우리는 큰 입력값에만 관심이 있기에, 이 방법을 사용하는 것이 매우 효율적이라 할 수 있다.
Order of growth classifications
아래와 같이, 대부분의 algorithm은 7가지로 분류된다.
| order of growth | name | description | tilde notation |
| $1$ | constant | statement | $\sim c$ |
| $\log N$ | logarithmic | divide in half | $\sim c \log N$ |
| $N$ | linear | loop | $\sim c N$ |
| $N \log N$ | linearithmic | divide and conquer | $\sim c N \log N$ |
| $N^2$ | quadratic | double loop | $\sim c N^2$ |
| $N^3$ | cubic | triple loop | $\sim c N^3$ |
| $2^N$ | exponential | check all subsets | $\sim c 2^N$ |
위 표에서 나타난 것처럼, quadratic 알고리즘부터는 입력값 크기가 큰 문제를 풀 수 없다. 즉, 문제를 scale할 수 없다.
예를 들어, 기술을 발전으로, cpu속도 10x 빨라졌고, memory크기가 10x 커졌다.
이때 각 알고리즘 문제 크기를 10배로 증가시켰을 때, 실행 시간의 변화를 살펴보자.
linear 알고리즘은 실행 시간이 그대로인 반면, quadratic 알고리즘은 실행 시간이 10배로 증가한다.
즉, 아무리 기술 발전을 해도, quadratic 알고리즘부터 풀 수 있는 문제 크기는 한정되어 있다.
Theory of algorithms
Types of analyses
입력에 따라 알고리즘 성능이 달라질 수 있다.
예를 들어, 입력에 따라 이진 탐색 성능이 $\sim 1$이 될 수 있고, $\sim \lg N$이 될 수 있다.
즉, 알고리즘 성능을 여러 방법으로 표현할 수 있다. 종류는 다음과 같이 3가지가 있다.
- Best case: "가장 쉬운" 입력이 주어졌을 때, 발생하는 실행 시간
- Worst case: "가장 어려운" 입력이 주어졌을 때, 발생하는 실행 시간
- Average case: "무작위" 입력이 주어졌을 때, 발생하는 실행 시간
대부분, worst case로 표현한다.
하지만, "가장 어려운" 입력이 거의 없다고 판단할 경우, average case를 제공하기도 한다.
Theory of algorithms
Goal: 문제의 "최적"의 algorithm(=성능 보장 및 lower bound)을 설계한다.
Approach
- 분석을 단순화한다.
- (새로운 알고리즘을 발견해) 문제의 상계(=upper bound)을 내린다. ← 상대적으로 쉽다.
- (증명을 통해) 문제의 하계(=lower bound)을 올린다. ← 상대적으로 매우 어렵다.
$U = \{1, 2, 3, 4, 5, 6\}, S = \{3, 4 \}$일 때, 상계는 $5, 6$이며, 하계는 $1, 2$다.
Memory
메모리 사용량(=memory usage)도 모델을 단순화하여 설계한다.
즉, 1. 메모리 사용량이 많은 자료구조 혹은 2. 빈도수가 높은 자료구조만 가지고 모델을 설계 한 후,
최고차항을 제외한 나머지를 없애버린다.
'Algorithm' 카테고리의 다른 글
| [Algorithm Part 1] 6. Balanced Search Tree (0) | 2023.04.10 |
|---|---|
| [Algorithm Part 1] 5. Symbol Table (0) | 2023.04.04 |
| [Algorithm Part 1] 4. PriorityQueue (0) | 2023.04.03 |
| [Algorithm Part 1] 3. Stack and Queue (0) | 2023.03.20 |
| [Algorithm Part 1] 1. Union-Find (0) | 2023.03.13 |