[DL] 7. How does DL solve problems?

이번 글에서는 딥러닝이 어떤 방식으로 문제를 접근하고 푸는지에 대해 자세히 살펴볼 것이다.

더 나아가, 딥러닝에 근간이 되는 이론이 무엇인지 살펴볼 것이다.

 

이진 분류 문제 풀이 방법

"임의의 키와 몸무게가 주어졌을 때 다이어트가 필요한지 혹은 필요하지 않은지를 판단"하는 문제를 풀어볼 것이다.

 

우선, 문제를 풀기 위해서는 문제를 정확히 이해하고, 이를 (수학적으로) 적절하게 재정의해야 한다.

위 문제를 독립 변수인 키/몸무게(=$x_1$, $x_2$)와 종속 변수인 다이어트 유무(=$y$) 간의 관계를 파악하는 것으로 재정의할 수 있다.

입력이 키/몸무게고 출력이 다이어트의 필요성 (or 확률)인 모델 (or 알고리즘)을 만든 후,

모델 출력인 $p$가 0.5보다 크면 다이어트가 필요한 것이고, 0.5보다 작으면 필요하지 않은 것으로 분류해 문제를 풀 것이다.

 

모델 추정 (DNN)

딥러닝으로 문제를 풀 때는 그에 맞는 적절한 DNN 구조를 설계하여 모델을 추정한다.

 

activation function: unit step function

(분류 기준선(경계선=$f(x_1,x_2)$)이 선형인) 선형 분류로 위 문제를 풀 수 있다고 가정하면,

활성화 함수가 계단 함수인 1층 (인공) 신경망 즉, 1층 퍼셉트론으로 입출력 간의 관계를 표현해볼 수 있다.

$$l=f(x_1,x_2)=b+w_1{x}_1+w_2{x}_2-(1.1)$$

$$p=h(l)=\{\begin{array}{ll}0,& (\text{if }l\le 0)\\ 1,& (\text{if }l>0)\end{array}-(1.2)$$

 

이를 3D로 표현하면 다음과 같다.

분류 기준선(회색 부분)은 선형이지만, 입출력($x$와 $y$) 간의 관계는 비선형임을 확인할 수 있다.

 

하지만, 위 방식은 여러 문제점이 존재한다.

1. 분류 경계선에서 미분이 불가능해 최적화 기법 중 하나인 경사 하강법을 사용하지 못한다.

2. 경계선 기준으로 값($p$=필요성 or 확률)이 너무 급변한다.

경계선을 살짝 넘었다고 확률이 0에서 1로 급변하는 것은 부자연스럽다. 

 

activation function: sigmoid function

unit step function의 문제점을 어느 정도 해소하기 위해,

활성화 함수를 보다 부드러운 sigmoid 함수($1/(1+e^{-x})$)를 바꿔 다음과 같이 수정할 수 있다.

$$l=f(x_1,x_2)=b+w_1{x}_1+w_2{x}_2-(2.1)$$

$$p=h(l)=\frac{1}{1+e^{(-l)}}-(2.2)$$

 

이를 3D로 표현하면 다음과 같다.

위와 마찬가지로, 분류 기준선은 선형이고, 입출력($x$와 $y$) 간의 관계는 비선형임을 확인할 수 있다.

 

하지만 위와 다르게, sigmoid 함수를 활성화 함수로 사용하면, 

1. 전구간에서 미분이 가능하다. (참고로, sigmoid 함수의 최대 기울기는 1/4이다.)

2. 경계선 기준으로 값이 보다 부드럽게 변한다.

$l$값에 따라 확률 $p$가 부드럽게 변하는 것이 자연스럽다.

 

더 중요한 것은 unit step function보다 합리적인 분류 기준선을 찾게 된다.

---

판단 기준 (손실 함수)

지금까지 문제에 맞게 DNN 구조를 설계해 모델을 추정했다. 이제부터는 데이터 기반$(x_i,y_i)$으로 최적의 파라미터 조합을 찾으면 된다.

딥러닝은 경사 하강법 (e.g., SGD, Adam)으로 손실값이 최소가 되는 최적의 파라미터 조합을 찾기 때문에, 판단 기준인 "손실 함수"만 문제에 맞게 잘 정의하면 된다.

 

그럼 이제부터 손실 함수를 정의해보겠다.

 

$p$를 확률로 정의했기 때문에, $y_i=1$이면 $p_i=1$을 출력하고, $y_i=0$이면 $p_i=0$을 출력하는 파라미터 조합을 찾는게 목표다.

 

sigmoid 함수를 활성화 함수로 사용한 경우 $p$의 최댓값은 1이고 최솟값은 0이기 때문에, 

모델은 $y_i=1$이면 $p_i$를 극대화하고, $y_i=0$이면 $p_i$를 극소화하는 파라미터 조합을 찾는 것으로 목표를 수정할 수 있으며, 수식으로 표현하면 다음과 같다. 

$$\text{if }{y}_i=1\text{then }\text{maximize }{p}_i,\text{else if }{y}_i=0\text{then }\text{minimize }{p}_i$$

이를 더 직관적으로 바꾸면 다음과 같다.

$$\text{maximize }{p}_i^{y_i}(1-p_i{)}^{1-y_i}$$

$p_i^{y_i}(1-p_i{)}^{1-y_i}$는 $y_i$일 확률을 의미한다. 

즉, $y_i=1$이면 다이어트할 확률($p_i$)을 의미하고, $y_i=0$이면 다이어트하지 않을 확률($1-p_i$)을 의미한다.

 

각각의 데이터 $(x_i,y_i)$는 독립적이기 때문에, 최종 목표는 $\prod _{i=1}^n{p}_i^{y_i}(1-p_i{)}^{1-y_i}$를 극대화하는 것이다.

하지만, 1보다 작은 값을 계속 곱하면 결국 0에 가까워지며, 이를 컴퓨터로 계산하면 underflow 문제가 발생한다.

그렇기 때문에, $\log$를 취해 곱하기($\times$)를 더하기($+$)로 바꿔 다음과 같이 표현할 것이다.

(단조 증가(monotonic increase)하기 때문에 바꿔도 가능하다.

쉽게 말해, 한쪽이 작아지면 다른쪽도 반드시 작아지고 한쪽이 커지면 다른쪽도 반드시 커지기 때문이다.)

$$\sum _{i=1}^n\log p_i^{y_i}(1-p_i{)}^{1-y_i}$$

 

ML에서는 일반적으로 값이 낮을수록 좋은 "손실 함수"를 판단 기준으로 사용하기 때문에, 위 수식에 -를 곱해 손실 함수로 사용할 것이며, 이를 Binary Cross Entropy라고 부른다.

$$\text{BCE}=-\sum _{i=1}^n{y}_i\log p_i+(1-y_i)\log (1-p_i)$$

---

logistic regression 

위 방식으로 이진 분류하는 것을 logistic regression이라고 한다.

"logit(=log-odd)인 $l$를 계산하는 것까지가 모델의 역할이고, 이후는 loss를 계산하기 위한 과정"으로 해석하면,

모델이 logit $l$를 linear regression($b+w_1{x}_1+w_2{x}_2$)으로 구해 이진 분류(if $l$ > 1 → diet($\hat{y}=1$), else if $l$ < 1 → no diet($\hat{y}=0$))했다고 볼 수 있기 때문이다.

즉, 분류 문제를 regression 문제로 바꿔 풀었다고 볼 수 있다. (regression에 대한 자세한 내용은 [ML] 2. Linear Regression에서)

참고로, odds는 "승산"을 의미한다. 승산이란 "어떤 사건이 발생할 확률(=$p$)과 발생하지 않을 확률(=$1-p$) 사이의 비율"을 의미하며, 수식으로는 $\frac{p}{1-p}$로 나타낸다.

sigmoid 함수의 진정한 의미

logit $l$에서 사건이 발생할 확률인 $p$를 얻기 위해서는 log-odd함수($=\log \frac{p}{1-p}$)의 역함수를 거쳐야 한다.

$$l=\log \frac{p}{1-p}\leftrightarrow p=\frac{1}{1+e^{-l}}$$

 

위에서 알 수 있듯이, logit $l$를 가지고 확률 $p$를 구해내는 식이 바로 sigmoid 함수다.

그래서, 이진 분류(YES/NO) 모델의 (마지막) 출력층 활성화 함수로 sigmoid 함수를 사용하는 것이다.

---

MSE(Mean Square Error) vs BCE(Binary Cross Entropy)

MSE를 이진 분류 손실 함수로 사용하면, BCE와 무엇이 다른지 살펴볼 것이다.

이진 분류의 MSE와 BCE은 각각 $(y_i-p_i{)}^2$와 $-(y_i\log p_i+(1-y_i)\log (1-p_i))$으로 표현 가능하다.

 

민감도

위 수식을 조건문으로 풀어쓰면 다음과 같다.

$$\text{ If }{y}_i=0\to \text{MSE}(p_i)=p_i^2\text{ and }\text{BCE}(p_i)=-\log (1-p_i{)}^2$$

$$\text{ Else if }{y}_i=1\to \text{MSE}(p_i)=(p_i-1{)}^2\text{ and }\text{BCE}(p_i)=-\log p_i^2$$

이를 그래프로 표현하면 다음과 같다.

 

왼쪽 그래프는 t=0인 경우, 오른쪽 그래프는 t=1인 경우

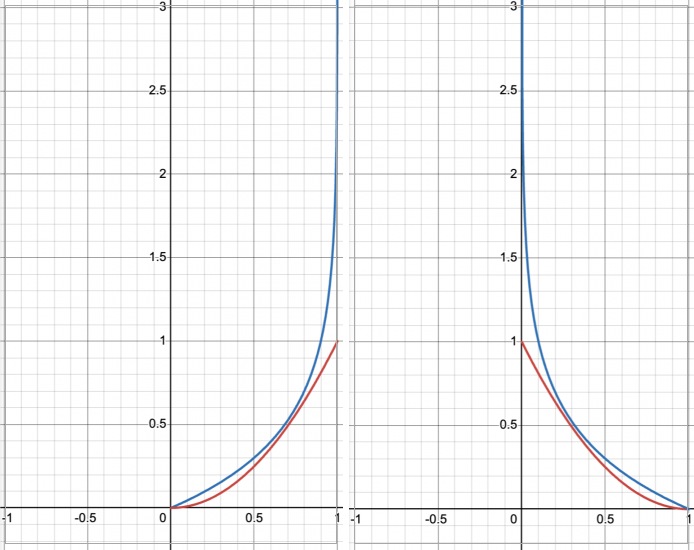
위 그래프에서 알 수 있을듯이, BCE(파란선)가 error에 훨씬 더 민감하다.

 

convex vs non-convex

출력층 파라미터 loss landscape의 개형이 MSE이면 non-convex, BCE이면 convex다.

 

이를 수식과 그래프로 표현하면 다음과 같다.

$${(\frac{1}{e^{-(b+w_1{x}_1+w_2{x}_2)}+1}-1)}^2-\log \frac{1}{e^{-(b+w_1{x}_1+w_2{x}_2)}+1}$$

빨간면 = MSE, 파란면 = BCE

 

위 그래프를 보면 알 수 있듯이, BCE는 어느 지점에서 시작해도 학습이 이루어진다. 즉, 최솟값으로 이동한다.

반면, MSE는 x, y 모두 큰 음수에서 시작하면 학습이 이루어지지 않는다. 즉, 최솟값으로 이동하지 않는다.

 

non-convexity

파라미터 loss landscape의 non-convexity가 MSE이면 높아지고, BCE이면 낮아진다.

 

당연하게도, 출력층으로부터 멀어질수록 non-convexity는 심해진다.

하지만, 출력층이 convex면 non-convexity가 덜 심해지기 때문이다.

 

위 내용을 표로 정리하면 다음과 같다.

		Binary Cross Entropy			Mean Squre Error
민감도		높다			낮다
출력층 loss landscape의 개형		convex			non-convex
은닉층의 non-convexity		낮다			높다

 

결론, 모든 면을 봤을 때 이진 분류에서는 BCE를 손실함수로 사용하는 것이 유리하다.

 

어떤 손실 함수를 사용할지는 선택의 영역이다.

하지만, 어떤 것을 선택하느냐에 따라 학습 난이도가 달라지기 때문에, 문제에 맞는 손실 함수를 선정해야 한다.

---

What is convex function?

convex 함수의 정의는 다음과 같고, 이를 만족하지 않은 함수를 non-convex 함수라고 부른다.

$$f(\alpha x+(1-\alpha )y)\le \alpha f(x)+(1-\alpha )f(y)(0\le \alpha \le 1\text{ and }x,y\in X)$$

쉽게 말해, convex 함수는 볼록 함수다.

그렇기 때문에, 경사 하강법에서 convex 함수가 유리하다. 어느 지점에서 시작해도 최솟값으로 수렴하기 때문이다.

반대로, non-convex 함수는 극솟값에 갇힐 수 있기 때문에 불리하다.

---

☆ DL Estimates $p_{Y|X}$ by MLE with DNN ☆ 

우리가 궁극적으로 알고자 하는 것은 "임의의 $x$가 입력으로 주어졌을 때 $y$의 분포" $p_{Y|X}(y|x)$이다. 

 

$p_{Y|X}(y|x)$를 구하는 방법은 다음과 같다.

1. 문제가 주는 정보 혹은 관찰을 통해 얻은 정보 $(x_1,y_1),(x_2,y_2),\cdots ,(x_n,y_n)$ 등을 기반으로 $p_{Y|X}(y|x)$가 어떤 분포 형태 (e.g., 베르누이 분포, 정규 분포)를 가질지 가설(=hypothesis)을 세운다.

2. 가설로 세운 분포의 모수(e.g., 베르누이 분포의 모수는 $p$, 정규 분포의 모수는 $\mu$, $\sigma$)를 추정(=estimate)한다.

 

이때, $x$와 $y$는 종속적이기 때문에 $x$에 따라 분포 $p_{Y|X}(y|x)$가 달라진다. 이는 $x$에 따라 모수가 달라짐을 의미한다. 

($x$ 변화에 따른 $p_{Y|X}(y|x)$ 변화가 모수 외의 것에서 발생한다면, 가설로 세운 분포와 다른 분포가 되기 때문이다.)

 

그렇기 때문에, 모수를 알기 위해서는 $x$와 모수 간의 관계를 파악해야 한다.

관계를 파악하는 방법은 다음과 같다.

1. 모수와 $x$ 간의 관계가 어떤 함수 형태($f_w$)를 가질지 가설을 세운다.

2. 가설로 세운 $f_w$의 매개변수를 추정하여 정확한 관계를 파악한다.

 

$f_w$로 모수를 구할 수 있기 때문에, 분포의 모수를 추정하는 것에서 $f_w$의 매개변수를 추정하는 것으로 문제를 바꿀 수 있다.

$$p_{Y|X}(y;{\theta }_x)\to p_{Y|X}(y;f_w(x))\to p_{Y|X}(y|x;w)$$

 

딥러닝은 $x$와 모수 간의 함수 형태를 인공 신경망으로 세우고, MLE(=NLL 최소화)로 $f_w$의 매개변수를 추정한다.

이를 수식으로 표현하면 다음과 같다.

$$\hat{w}=\underset{w}{\text{argmin}}-\sum _{i=1}^n\log p_{Y|X}(y_i|x_i;w)$$

 

위 수식은 "모수가 $f_w(x_i)$인 확률분포 $p_{Y|X}$에서 $y_i$가 나올 확률을 극대화하는 $\hat{w}$을 구하는 식"이다.

일반적으로, 이렇게 추정한 $\hat{w}$로 $p_{Y|X}$ 혹은 대푯값(e.g., 평균, 분산, 중앙값)을 구한다.

 

결론, 딥러닝은 인공 신경망으로 구성된 MLE 기계다.

 

Exmple

분포 $p_{Y|X}$가 베르누이 분포이고 모수 $p$가 $f_w(x_i)$라고 가정하면, 

$p_{Y|X}(y_i|x_i;w)=(1-f_w(x_i){)}^{(1-y_i)}+f_w(x_i{)}^{y_i}$로 표현할 수 있다.

분포 $p_{Y|X}$가 정규 분포이고, 모수 $\mu$가 $f_w(x_i)$이고, $\sigma$는 $x_i$와 독립적이라고 가정하면, 

$p_{Y|X}(y_i|x_i;w)=\frac{1}{\sigma \sqrt{2\pi }}{e}^{\frac{-(y_i-f_w(x_i){)}^2}{2{\sigma }^2}}$로 표현할 수 있다.

 

이를 각각 NLL(Negative Log Likelihood function)로 바꾸면, $\sum _{i=1}^n-(y_i\log f_w(x_i)+(1-y_i)\log (1-f_w(x_i)))$와 $\sum _{i=1}^n(y_i-f_w(x_i){)}^2$이 되며,

이는 앞에서 살펴본 대표적인 손실 함수 BCE와 MSE다.

 

즉, 손실함수는 $p_{Y|X}$가 어떤 분포 형태를 가질지, 모수와 $x$ 간의 관계가 어떤 함수 형태를 가질지에 따라 달라진 것이지 이 모두 NLL이라는 뿌리에서 기반된 것이다.

그러므로, "문제에 맞는 손실 함수를 찾는 과정"은 "문제 상황에 맞는 $p_{Y|X}$와 ${\theta }_x=f_w(x)$를 찾는 과정"과 동일하다고 볼 수 있다.

 

$p_{Y|X}$ 분포 형태만 고려했을 때,

이진 분류에는 확률변수 $Y$가 취할 수 있는 값이 두 개(O/X)이기 때문에, $P_{Y|X}$를 정규 분포가 아닌 베르누이 분포로 가정하는 것이 적절하다.

반대로, 회귀 문제에서는 확률 변수 $Y$가 취할 수 있는 값이 연속적이기 때문에, $P_{Y|X}$를 정규분포로 가정하는 것이 적절하다.

---

다중 분류 문제 풀이 방법

"임의의 키와 몸무게가 주어졌을 때 어떤 체중상태(과체중, 정상체중, 저체중)인지를 판단"하는 문제를 풀어볼 것이다.

 

이진 분류와 마찬가지로, 문제를 풀기 위해서는 문제를 정확히 이해하고, 이를 (수학적으로) 적절하게 재정의해야 한다.

위 문제를 독립 변수인 키/몸무게(=$x_1$, $x_2$)와 종속 변수인 체중상태(=$y$) 간의 관계를 파악하는 것으로 재정의할 수 있다.

입력이 키/몸무게고 출력이 체중 상태의 확률분포(과체중/정상체중/저체중)인 모델 (or 알고리즘)을 만든 후,

모델 출력인 $\mathbf{p}=\left[\begin{array}{c}{p}_1\\ p_2\\ p_3\end{array}\right]$에서 확률값이 가장 높은 체중 상태로 분류해 문제를 풀 것이다.

참고로, $p_1$, $p_2$, $p_3$은 각각 과체중, 정상체중, 저체중 확률을 의미하고, $y=1$이면 과체중, $y=2$이면 정상체중, $y=3$이면 과체중을 의미한다. 

모델 추정 (DNN)

딥러닝으로 문제를 풀 때는 그에 맞는 적절한 DNN 구조를 설계하여 모델을 추정한다.

 

activation function: softmax function

이진 분류와는 다르게 다중 분류에서는 출력층 노드 수를 범주(=class) 수 만큼 늘려야 한다.

그리고, 확률분포가 출력될 수 있도록 출력층의 활성화 함수로 softmax 함수$\left(\frac{e^{x_i}}{\sum _{j=1}^m{e}^{x_j}}\right)$를 사용할 것이다.

 

이진 분류 때와 동일하게, 1층 (인공) 신경망으로 입출력 관계를 표현하면 다음과 같다.

$$\mathbf{l}=f(x_1,x_2)=\mathbf{b}+{\mathbf{w}}_{\mathbf{1}}{x}_1+{\mathbf{w}}_{\mathbf{2}}{x}_2({\mathbf{w}}_{\mathbf{1}}=\left[\begin{array}{c}{w}_{11}\\ w_{12}\\ w_{13}\end{array}\right],{\mathbf{w}}_{\mathbf{2}}=\left[\begin{array}{c}{w}_{21}\\ w_{22}\\ w_{23}\end{array}\right],\mathbf{b}=\left[\begin{array}{c}{b}_1\\ b_2\\ b_3\end{array}\right],\mathbf{l}=\left[\begin{array}{c}{l}_1\\ l_2\\ l_3\end{array}\right])-(3.1)$$

$$p_i=h(l_i)=\frac{e^{l_i}}{\sum _{j=1}^m{e}^{l_j}}-(3.2)$$

 

Why not $\frac{|x_i|}{\sum _{j=1}^m|x_j|}$?

확률분포가 되기 위해서는 두 가지 조건을 충족해야 한다.

첫번째, 모든 출력값이 0보다 크거나 같아야 한다. 두번째, 출력값의 합이 1이어야 한다.

$\frac{|x_i|}{\sum _{j=1}^m|x_j|}$은 이 두 가지 조건을 충족하기 때문에 softmax 함수 대신 사용 가능하다.

 

하지만, 위 함수는 입력값으로 1, 1, 1과 1, -1, 1이 들어왔을 때 이를 구분하지 못한다. 즉, 의미가 중복되는 영역이 많다. 다시 말해, 활용하지 못하는 영역이 많다.

반대로, softmax 함수는 입력마다 다른 값을 출력한다. 즉, 각 영역은 서로 다른 의미를 가지고 있다. 다시 말해, 모든 영역을 활용한다.

 

softmax vs sigmoid

softmax는 출력값을 묶어서 하나의 확률분포($\sum _{i=1}^m{p}_i=1$) 보는 반면, sigmoid는 출력값을 개별적인 확률값($\sum _{i=1}^m{p}_i\ne 1$)으로 본다.

그렇기 때문에, softmax의 경우 임의의 출력값이 증가하면 필연적으로 다른 출력값이 감소하는 반면, sigmoid의 경우 임의의 출력값이 다른 출력값에 영향을 주지 않는다.

 

쉽게 말해, 다중 분류에서 sigmoid 함수를 사용하는 것은 "m개의 이진 분류 모델이 각 class가 나올 확률을 출력하는 방식"이다.

 

그렇기 때문에, softmax 함수가 multi-classification 문제에 더 적합하고, sigmoid 함수는 multi-label classification에 적합한 것이다.

---

판단 기준 (손실 함수)

모델 출력을 각 class의 확률로 정의했기 때문에, $p_{i,h}$만 1을 출력하고 나머지 $p_{i,j}$는 0을 출력하는 파라미터 조합을 찾는게 목표다.

($p_{i,j}$는 "i번째 데이터의 출력값인 벡터 $p_i$의 j번째 index"를 의미하고, $h$는 hot-index를 의미한다.)

 

softmax 함수를 활성화 함수로 사용한 경우 $p$의 최댓값은 1이고 최솟값은 0이기 때문에, 

모델은 $p_{i,h}$을 극대화하고 나머지 $p_{i,j}$는 극소화하는 파라미터 조합을 찾는 것으로 목표를 수정할 수 있으며, 수식으로 표현하면 다음과 같다. 

$$\text{maximize }{p}_{i,h}\text{ and }\text{maximize }{p}_{i,j}$$ 

이를 더 직관적으로 바꾸면 다음과 같다.

$$\text{maximize }{p}_{i,h}$$

$\sum _{j=1}^m{p}_{i,j}=1$이기 때문에, $p_{i,h}$가 증가하면 필연적으로 나머지 $p_{i,j}$는 감소할 수 밖에 없다.

 

이 수식에 $-\log$를 취한 후, 모든 데이터에 고려하여 수식을 수정하면 다음과 같은 손실 함수가 나오며, 이를 Cross Entropy라 부른다.

$$\text{CE}=-\sum _{i=1}^n\log p_{i,h}$$

 

정보 이론 관점

손실 함수가 cross-entropy이면, cross-entropy가 최소화하는 방향으로 학습이 진행된다.

$$-y_1\log y_1-y_2\log y_2-y_3\log y_3\le -y_1\log p_1-y_2\log p_2-y_3\log p_3$$

위 수식처럼 cross-entropy는 무조건 entropy 보다 크기 때문에,

"cross-entropy를 줄인다"는 것은 "cross-entropy를 entropy에 점점 가깝게 만든다"는 것을 의미이다.

$p_i$가 $y_i$와 가까워져야만 cross-entropy가 entropy에 점점 가까워지기 때문에, 

"cross-entropy가 entropy에 점점 가까워진다"는 것은 "분포 p가 분포 y에 점점 가까워짐"을 의미한다.

결론, "cross-entropy를 손실 함수로 삼았다"는 것은 "분포 p를 열심히 바꿔 분포 y와 같도록 하겠다"는 의도가 있다.

 

cross-entropy를 다중 분류 손실 함수로 사용하면, cross-entropy와 entropy의 관계는 다음과 같다.

$$0\le -\log p_h,(h\text{ is hot-index})$$

즉, 나머지 $p_j$는 고려하지 않고 오직 $p_h$만 1에 가까워지도록 학습이 진행된다..

이것만으로도 분포 p를 분포 y에 가깝게 만들 수 있다. $p_h$가 증가하면 필연적으로 나머지 $p_j$가 감소할 수 밖에 없기 때문이다.

---

다중 분류도 MLE다

다중 분류는 분포 $p_{Y|X}$를 multinoulli 분포로, 모수 $p_j$를 "$f_w(x_i)$의 $j$번째 요소"로,  $[o_1,o_2,\cdots ,o_m]$을 $y_i$의 one-hot vector로 가정하고, 이를 MLE(min NLL)로 매개변수를 추정한다.

 

분포 $p_{Y|X}$는 다음과 같이 표현할 수 있다.

$$p_{Y|X}(y_i|x_i;w)=\prod _{j=1}^m{p}_j^{o_j}$$

 

이를 NLL로 바꾸면, $-\sum _{i=1}^n\log p_h,(h\text{ is hot-index})$이 되며, 이를 cross-entropy라 부른다.

---

softmax regression 

위 방식으로 다중 분류하는 것을 softmax regression이라고 한다.

"logit(=log-odds)인 $l$를 계산하는 것까지가 모델의 역할이고, 이후는 loss를 계산하기 위한 과정"으로 해석하면,

모델이 logit $\mathbf{l}$를 regression($\mathbf{b}+{\mathbf{w}}_1{x}_1+{\mathbf{w}}_2{x}_2$)으로 구해 다중 분류($\hat{y}=\text{argmax }\mathbf{l}$)했다고 볼 수 있기 때문이다.

즉, 다중 분류 문제도 regression 문제로 바꿔 풀었다고 볼 수 있다. (regression에 대한 자세한 내용은 [ML] 2. Linear Regression에서)

참고로, 다중 분류에서의 odd는 "$i$ 범주일 확률과 기준 범주(=baseline category)일 확률 사이의 비율"을 의미하며, 수식으로는 $p_i/p_t,(t\text{ is baseline category})$로 나타낸다. 

softmax 함수의 진정한 의미

logit $\mathbf{l}$에서 확률인 $\mathbf{p}$를 얻기 위해서는 log-odd함수($=\log (p_i/p_t)$)의 역함수를 거쳐야 한다.

$$l_i=\log \frac{p_i}{p_t}\leftrightarrow p_i=\frac{e^{l_i}}{\sum _{j=1}^m{e}^{l_j}},(t\text{ is baseline category})$$

 

위에서 알 수 있듯이, 다중 분류에서 logit $\mathbf{l}$를 가지고 확률 $\mathbf{p}$를 구해내는 식이 바로 softmax 함수다.

그래서, 다중 분류 모델의 (마지막) 출력층 활성화 함수로 softmax 함수를 사용하는 것이다.