2024. 4. 24. 22:58ㆍRL
이전 글에서 DP 기법으로 최적 가치 함수와 최적 정책을 구해봤다.
DP를 이용하려면 환경 모델을 알고 있어야 한다.
하지만 안타깝게도, 현실에는 환경 모델을 알 수 없는 경우가 대부분이다.
환경 모델이 알려진 경우에는 에이전트 측에서 실제로 행동하지 않고 '상태, 행동, 보상'의 전이를 시뮬레이션할 수 있지만,
이런 경우에는 에이전트가 실제로 행동을 취해 얻은 경험(상태, 행동, 보상)을 토대로 최적 가치 함수와 최적 정책을 구해야 한다.
이번 글의 목표는 에이전트가 실제로 행동을 취해 얻은 경험을 바탕으로 가치 함수를 추정하고 이를 기반으로 최적 정책을 찾는 것이다.
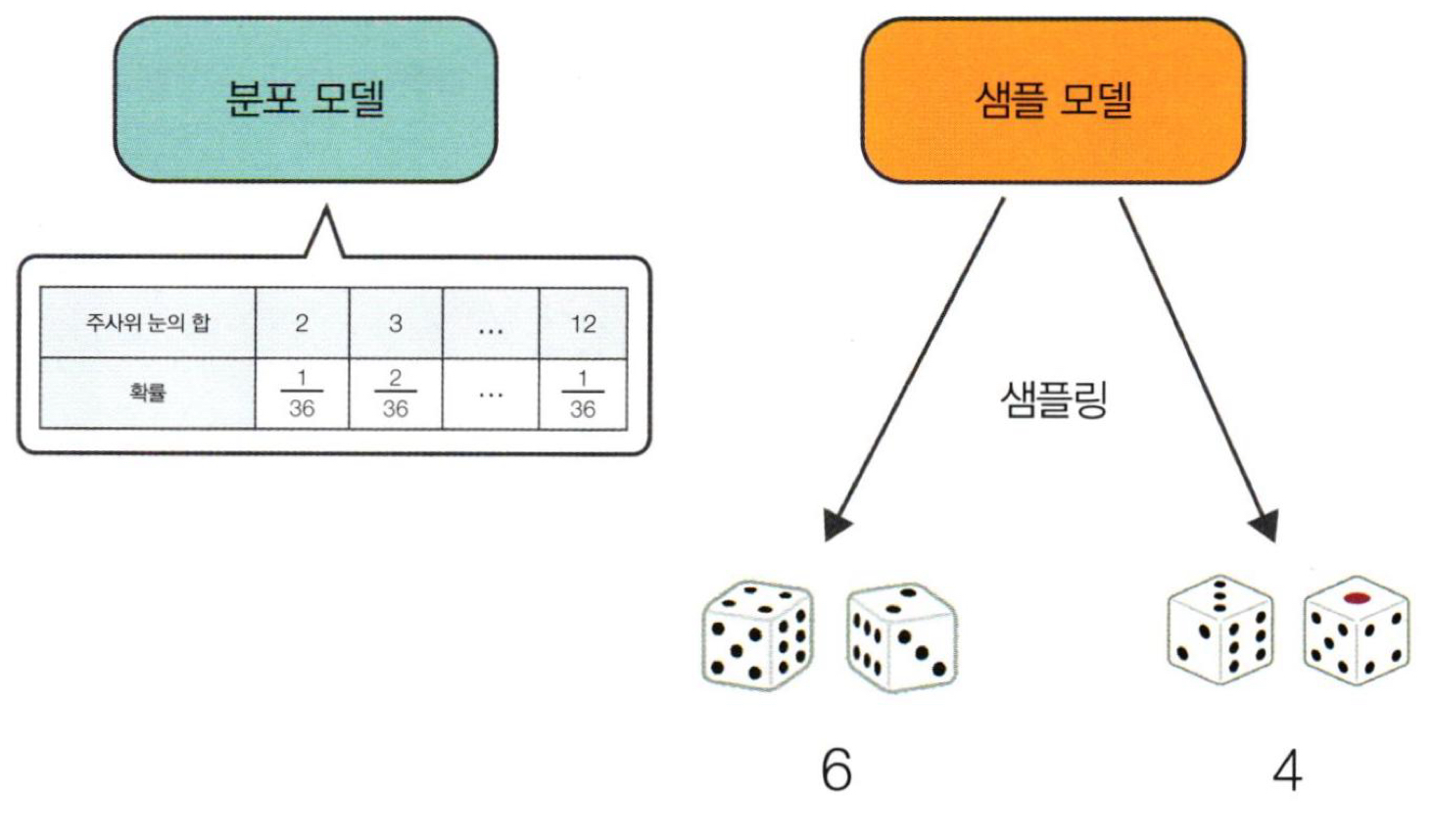
분포 모델(distribution model) vs 샘플 모델(sample model)
분포 모델은 확률 분포를 표현한 모델이다.
샘플 모델은 표본(sample)을 추출하는 모델이다.
몬테가를로법이란?
몬테가를로법은 데이터를 반복적으로 샘플링(추출)하여 얻은 결과를 토대로 얻고자 하는 값(numerical results)을 추정하는 기법이다.
강화학습에 몬테가를로법을 활용하면, (에이전트가 실제로 행동을 취해 얻은) 경험(=데이터)을 바탕으로 가치 함수(=numerical result)를 추정할 수 있게 된다.
몬테가를로법으로 정책 평가
가치 함수는 수익의 기댓값이다.
기댓값은 큰 수의 법칙에 의해 몬테가를로법으로 추정할 수 있다.
다시 말해, 샘플 데이터를 많이 수집해 평균을 내면 실제 기댓값을 추정할 수 있다.
그렇기 때문에, 에피소드를 반복적으로 진행하면서 수익 데이터를 수집한 후, 데이터의 평균을 계산해 실제 가치 함수 $v_\pi$를 추정하는 몬테가를로법을 강화학습에 적용할 수 있다.
(참고로, 수익 데이터를 수집해야 하기 때문에 일회성 과제만 몬테가를로법을 사용할 수 있다.)
큰 수의 법칙에 가치 함수를 대입하여 표현하면 다음과 같다.
$$v_\pi(s) = \mathbb E_\pi[G|s]$$
$$V_\pi^n(s) = {G_s^{1} + G_s^{2} + \cdots + G_s^{n} \over n}$$
$$V_\pi^n(s) = V_\pi^{n-1}(s) + \frac{1}{n}(G_s^n - V_\pi^{n-1}(s))$$
$$v_\pi(s) = \lim_{n \rightarrow \infty} V_\pi^n(s)$$
($G_s^{i}$는 $i$번째 에피소드에서 상태 $s$에서 시작해 얻은 수익을 의미한다.)
모든 상태의 가치 함수를 구하기 위해서는 각 상태를 시작 위치로 설정하여 에피소드를 진행한 다음, 시작 위치의 수익을 구해 시작 위치의 가치 함수를 갱신해야 한다.

하지만, 이 방법은 매우 비효율적일 뿐만 아니라, 시작 위치를 임의로 설정할 수 있는 시뮬레이터만 가능하다. 대부분 경우 임의로 시작 위치를 설정할 수 없다.
시작 위치가 고정되어 있어도 에피소드가 진행되는 동안 여러 상태를 경유하기 때문에, 시작 위치의 수익에서 경유한 위치의 수익을 구할 수 있어 경유한 상태의 가치 함수를 모두 갱신하여 효율을 높일 수 있다.

반면에 경로를 경유한 상태의 가치 함수만 갱신된다는 단점이 있다.
탐욕화로 정책 제어
평가 단계에서는 몬테가를로법으로 이용해 $v_\pi$를 추정했고, 이제 개선 단계에서는 탐욕화로 정책을 개선하면 된다.
탐욕화를 수식으로 표현하면 다음과 같다.
$$\begin{matrix} \mu(s) &=& \underset{a}{\text{argmax }} q(s, a) \\ &=& \underset{a}{\text{argmax }}R_s^a + \gamma \sum_{s^\prime} P_{ss^\prime}^a v(s^\prime) \end{matrix}$$
이때, 상태 가치 함수를 사용해 정책을 개선하기 위해선 환경 모델을 알아야 하기 때문에 행동 가치 함수로 정책을 개선해야 한다.
그래서, 상태 가치 함수를 평가하는 대신 행동 가치 함수를 평가해야 한다.
그러려면, 몬테카를로법의 갱신식 다음과 같이 수정해야 한다.
$$q_\pi(s, a) = \mathbb E_\pi[G|s, a]$$
$$Q_\pi^n(s, a) = {G_{(s,a)}^{1} + G_{(s,a)}^{2} + \cdots + G_{(s,a)}^{n} \over n}$$
$$Q_\pi^n(s, a) = Q_\pi^{n-1}(s, a) + \frac{1}{n}(G_{(s,a)}^n - Q_\pi^{n-1}(s, a))$$
$$q_\pi(s, a) = \lim_{n \rightarrow \infty} Q_\pi^n(s, a)$$
개선 사항 1. 탐욕 정책 → $\epsilon$-탐욕 정책
정책 개선 때는 탐욕화로 경로가 한 가지로 고정되고 정책 평가 때는 경로를 경유한 행동 가치 함수만 갱신하기 때문에, 모든 행동 가치 함수를 갱신할 수 없게 된다.
쉽게 말해, 경로에 포함된 ($s$, $a$) 조합만 실제 q-함수에 근사됐다는 의미다.

그래서, 실제로 행동을 할 때 $\epsilon$-탐욕 정책을 사용해 일정 확률로 탐욕 행동 외의 행동(=탐색)을 하도록 강제했다.

다시 말해, 탐욕화가 아닌 $\epsilon$-탐욕화으로 정책을 갱신하도록 수정했다.
$$\mu(s) = \begin{cases} \underset{a}{\text{argmax }} q(s, a),& \text{if } 1-\epsilon \\ \text{otherwise},& \text{if } \epsilon \end{cases}$$
이는 탐욕 경로에 포함되지 않는 상태/행동 조합에 방문해 해당 조합의 행동 가치 함수를 갱신시켜준다.
하지만, 탐욕 정책으로 행동하지 않기 때문에 부정확한 q-함수값을 구하는 단점이 있다.
개선 사항 2. 표본 평균($1/n$) → 지수 평균 이동(고정값 $\alpha$)
매 에피소드가 끝날 때마다 평가와 개선을 한번씩 수행하면서 최적 정책을 찾는다.
즉, 에피소드가 끝날 때마다 정책이 개선된다.
그럼, 과거 데이터보다 최신 데이터가 현재 정책과 흡사하기 때문에 더 많은 가중치를 줘야 한다.
그래서, 모든 수익 데이터에 균일한 가중치를 주는 표본 평균 대신, 최신 데이터 더 많은 가중치를 주는 지수 이동 평균을 사용할 것이다.
이를 수식으로 표현하면 다음과 같다.
$$Q_\pi^n(s, a) = Q_\pi^{n-1}(s, a) + \frac{1}{n}(G_{(s,a)}^n - Q_\pi^{n-1}(s, a)) \rightarrow Q_\pi^n(s, a) = Q_\pi^{n-1}(s, a) + \alpha(G_{(s,a)}^n - Q_\pi^{n-1}(s, a))$$
MC법의 알고리즘
1. 정책 $\pi$로 에피소드를 진행하여, 데이터$[(S_1, A_1, G_1), (S_2, A_2, G_2), \cdots, (S_n, A_n, G_n)]$를 추출한다.
$$\pi(a|S_t) = \begin{cases} \underset{a}{\text{argmax }} Q_\pi(S_t, a),& \text{if } 1-\epsilon \\ \text{otherwise},& \text{if } \epsilon \end{cases}$$
2. 각 $(S_t, A_t, G_t)$로 $Q_\pi^\prime(S_t,A_t)$를 갱신한다.
$$Q_\pi^\prime(S_t, A_t) = Q_\pi(S_t, A_t) + \alpha(G_t- Q_\pi(S_t, A_t))$$
3. 갱신된 $Q_\pi^\prime(S_t,A_t)$으로 정책 $\pi$을 개선한다.
$$\pi^\prime(a|S_t) = \begin{cases} \underset{a}{\text{argmax }} Q_\pi^\prime(S_t, a),& \text{if } 1-\epsilon \\ \text{otherwise},& \text{if } \epsilon \end{cases}$$
이때, 위 연산 1번 구간에서 동일하게 다시 수행하기 때문에 생략 가능하다.
그리고 $Q_\pi$가 있으면 $\pi$을 굳이 저장하지 않아도 된다.
'RL' 카테고리의 다른 글
| [RL] 6. DQN(Deep Q Network) (0) | 2024.04.28 |
|---|---|
| [RL] 5. Temporal Difference: SARSA, Q-learning (0) | 2024.04.26 |
| [RL] 3. DP: policy iteration, value iteration (0) | 2024.04.23 |
| [RL] 2. Bellman equation (0) | 2024.04.23 |
| [RL] 1. Markov Decision Chain (0) | 2024.04.20 |