[RL] 5. Temporal Difference: SARSA, Q-learning

몬테카를로법을 이용하면 환경 모델 없이도 정책을 평가할 수 있다.

하지만, 몬테카를로법은 에피소드의 끝에 도달한 후에야 가치 함수를 갱신할 수 있다.

그렇기 때문에, 지속적 과제에서는 몬테카를로법을 사용할 수 없다. 또한 일회성 과제더라도 완료까지 시간이 꽤 걸리는 과제라면 몬테카를로법으로 가치 함수를 갱신하는데 오랜 시간이 소모되기 때문에 적합하지 않다.

 

이번 글에서는 환경 모델을 사용하지 않을 뿐 아니라 행동을 한 번 수행할 때마다 가치 함수를 갱신하는 TD(Temporal Difference) 기법에 대해 알아볼 것이다.

 

TD법은 MC(Monte Carlo)법과 DP(Dynamic Programming)법을 합친 기법이다.

직관적으로, TD법은 DP법처럼 추정치로 추정치를 갱신하고, MC법처럼 환경 모델에 대한 정보가 없이 샘플 데이터만으로 가치 함수를 갱신한다.

TD법은 환경 모델에 대한 정보가 필요 없는 MC 갱신식을 사용하는 대신 $G_t$ 말고 $R_t + \gamma V_\pi(S_{t+1})$로 사용해 다음 가치 함수의 추정치를 사용해 현재 가치 함수의 추정치를 갱신한다.

TD 정책 평가 갱신식 유도

$$v_\pi(v) = \mathbb E_\pi[G_t|S_t=s] \rightarrow V_\pi^\prime(S_t) = V_\pi(S_t) + \alpha\{G_t - V_\pi(S_t)\} - (1)$$

$$\begin{matrix} v_\pi(s) &=& \sum_{a} \pi(a|s)\left(R_{s}^a + \gamma \sum_{s^\prime} P_{ss^\prime}^a v_\pi(s^\prime)\right) \\ &=& \sum_a \pi(a|s) R_s^a + \gamma \sum_a \sum_{s^\prime} P_{ss^\prime}^a v_\pi(s^\prime) \\ &=&  \mathbb E_\pi[R_t|S_t=s] + \gamma \mathbb E_\pi[v_\pi(S_{t+1})|S_t=s] \\ &=& \mathbb E_\pi[R_t + \gamma v_\pi(S_{t+1})|S_t=s] - (2) \end{matrix}$$

$$v_\pi(v) = \mathbb E_\pi[R_t + \gamma v_\pi(S_{t+1})|S_t=s] \rightarrow V_\pi^\prime(S_t) = V_\pi(S_t) + \alpha\{R_t + \gamma V_\pi(S_{t+1}) - V_\pi(S_t)\} - (3)$$

(1)번은 MC법, (2)번은 DP법, (3)번은 TD법

 

여기서, $R_t + \gamma V_\pi(S_{t+1})$를 TD 목표(TD target)라고 하며, TD법은 $V_\pi(S_t)$를 TD 목표 방향으로 갱신한다고 볼 수 있다.

MC vs TD

환경 모델을 모를 때 사용할 수 있는 기법으로는 MC와 TD가 있다.

지속적인 과제라면 TD법 이외에는 대안이 없지만, 일회성 과제라면 무엇이 더 나은 선택지일까?

이론적으로 어느 쪽이 항상 나은지는 증명되지 않았지만, 일반적으로 현실의 많은 문제에서는 TD법이 더 빠르게 학습한다.

MC법과 TD법이 무엇을 목표로 하는지 보면 그 이유를 알 수 있다.

$$V_\pi^\prime(S_t) = V_\pi(S_t) + \alpha\{R_t + \gamma V_\pi(S_{t+1}) - V_\pi(S_t)\} - \text{TD}$$

$$V_\pi^\prime(S_t) = V_\pi(S_t) + \alpha\{G_t - V_\pi(S_t)\} - \text{MC}$$

 

$G_t$를 얻기 위해선 에피소드를 끝내야 하지만, $R_t + \gamma V_\pi(S_{t+1})$는 한 타임스텝만 거치면 구할 수 있다.

즉, MC법은 에피소드가 끝나야 갱신이 되는데 TD법은 타임스텝마다 갱신하기 때문에 효율적인 학습을 기대할 수 있다.

 

$G_t$는 많은 시간을 쌓아 얻은 결과이기 때문에 분산(=변동)이 큰다.

반면, $R_t + \gamma V_\pi(S_{t+1})$는 오직 한 타임스텝으로 얻은 결과이기 때문에 분산(=변동)이 작다.

물론, $V_\pi(S_{t+1})$는 추정치이기 때문에 "편향(bias)"이 존재한다. 하지만, 편향은 갱신을 반복할수록 0에 수렴하기 때문에 큰 문제가 되지 않는다.

참고로, $G_t$는 실제값이기 때문에 편향이 없다.

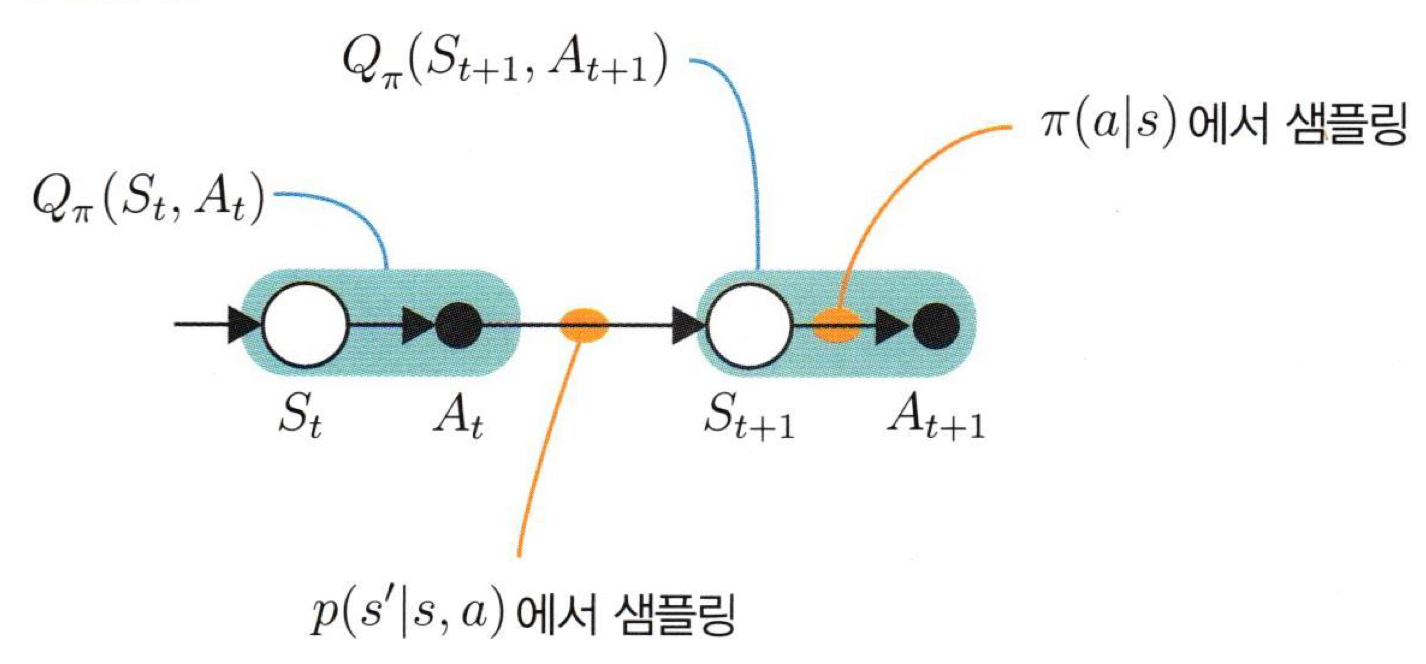
SARSA (TD법 + $\epsilon-$탐욕 정책)

TD법으로 행동 가치 함수를 갱신하고 $\epsilon$-탐욕화로 정책 $\pi$를 개선하면 이를 SARSA라고 한다.

정책 평가와 정책 제어를 수식으로 표현하면 다음과 같다.

$$Q_\pi^\prime(S_t,A_t) = Q_\pi(S_t, A_t) + \alpha\{R_t + \gamma Q_\pi(S_{t+1}, A_{t+1}) - Q_\pi(S_t, A_t)\}$$

$$\pi(a|s) = \begin{cases} \underset{a}{\text{argmax }} Q_\pi(s, a),& \text{if } 1-\epsilon \\ \text{otherwise},& \text{if } \epsilon \end{cases}$$

 

SARSA 알고리즘은 다음과 같다.

1. 정책 $\pi$로 데이터[$S_t$, $A_t$, $R_t$, $S_{t+1}$, $A_{t+1}$]를 추출한다.

$$\pi(a|S_t) = \begin{cases} \underset{a}{\text{argmax }} Q_\pi(S_t, a),& \text{if } 1-\epsilon \\ \text{otherwise},& \text{if } \epsilon \end{cases}$$

 

2. [$S_t$, $A_t$, $R_t$, $S_{t+1}$, $A_{t+1}$]로 $Q(S_t, A_t)$를 갱신한다.

$$Q_\pi^\prime(S_t,A_t) = Q_\pi(S_t, A_t) + \alpha\{R_t + \gamma Q_\pi(S_{t+1}, A_{t+1}) - Q_\pi(S_t, A_t)\}$$

 

3. 갱신된 $Q_\pi^\prime(S_t, A_t)$으로 정책 $\pi$을 개선한다.

$$\pi^\prime(a|S_t) = \begin{cases} \underset{a}{\text{argmax }} Q_\pi^\prime(S_t, a),& \text{if } 1-\epsilon \\ \text{otherwise},& \text{if } \epsilon \end{cases}$$

이때, 1번 구간과 3번 구간은 동일한 연산을 수행하기 때문에, 위 구간은 생략해도 된다.

그리고 $Q_\pi$가 있으면 $\pi$를 굳이 저장하지 않아도 된다.

off-policy

SARSA는 TD법과 $\epsilon$-탐욕 정책을 결합해 최적 정책을 찾았다.

하지만, 엄밀히 말하자면, 최적에 가까운 정책이지 완벽한 최적 정책이 아니다.

탐욕적으로 행동하지 않아 부정확한 q-함수값을 구했기 때문이다.

하지만, 탐욕적으로 행동하면 탐욕 경로에 포함된 ($s$, $a$) 조합의 q-함수값만 업데이트 된다.

 

우리가 원하는 것은 모든 ($s$, $a$) 조합의 q-함수를 정확히 업데이트하는 것이다.

이때, 등장한 개념이 바로 오프-정책이다.

 

에이전트가 실제로 행동을 취할 때 사용하는 정책을 행동 정책(behavior policy)이라 하고,

평가와 개선을 할 때 사용되는 정책을 대상 정책(target policy)이라 한다.

 

이때, 행동 정책과 대상 정책을 동일시하는 경우를 온-정책(on-policy)이라고 하고, 구분한 경우를 오프-정책(off-policy)이라고 한다.

지금까지 살펴본 모든 기법들은 온-정책을 사용한 것이다.

오프-정책은 행동 정책으로 이동 경로 ($s$, $a$)를 결정하고, 대상 정책으로 ($s$, $a$)조합의 행동 가치 함수를 갱신하고 갱신된 행동 가치 함수로 기존 대상 정책을 개선한다.

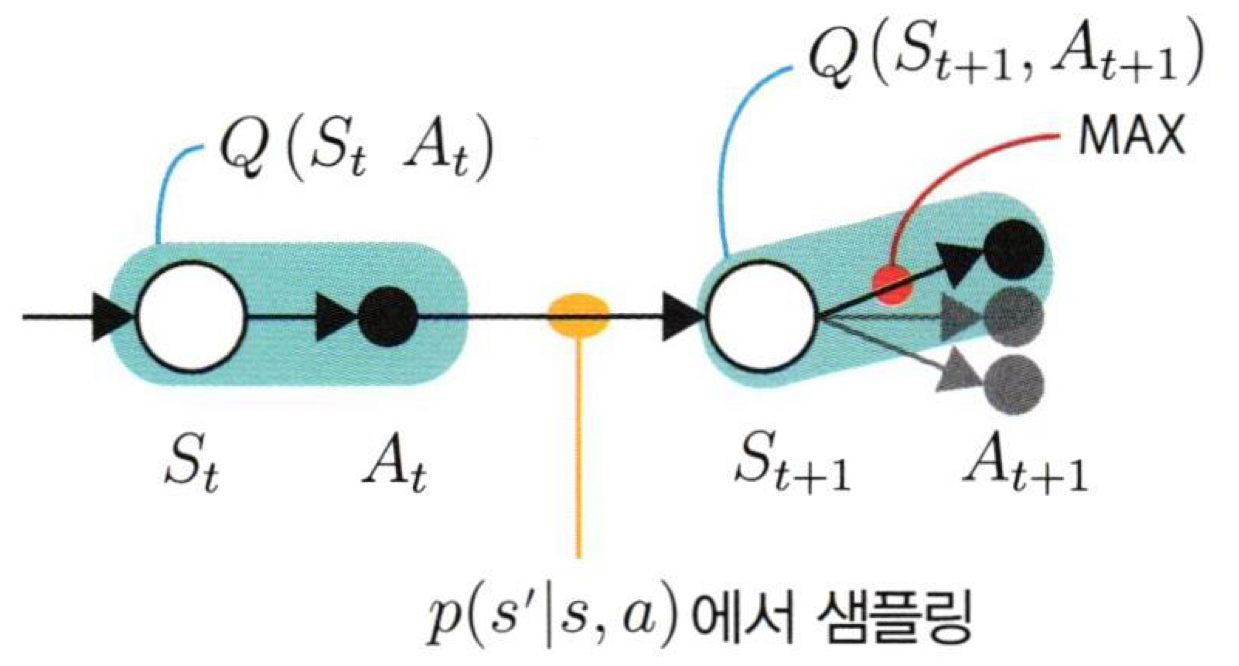
Q-learning (TD법 + off-learning)

행동 정책은 모든 ($S_t$, $A_t$) 조합을 골고루 볼 수 있기 때문에 $\epsilon$-탐욕 정책을 사용해야 하고, 대상 정책은 행동 가치 함수를 정확하게 갱신해야 하기 때문에 탐욕 정책을 사용해야 한다.

 

결론, $\epsilon$-탐욕 정책 $\pi$으로 이동 경로($S_t$, $A_t$)를 결정하지만, ($S_t$, $A_t$) 조합의 행동 가치 함수 $Q(S_t, A_t)$는 탐욕 정책 $\mu$으로 갱신하고, 갱신된 $Q^\prime(S_t, A_t)$로 다시 탐욕 정책을 개선한다. 이 기법을 Q-learning이라고 한다.

 

Q-learning 알고리즘은 다음과 같다.

1. 행동 정책인 $\epsilon$-탐욕 정책 $\pi$로 이동 경로 ($S_t$, $A_t$) 정한다.

$$\pi(a|S_t) = \begin{cases} \mu(S_t),& \text{if } 1-\epsilon \\ \text{otherwise},& \text{if } \epsilon \end{cases}$$

 

2. $Q(S_t, A_t)$를 갱신하기 위해 대상 정책인 탐욕 정책 $\mu$로 ($S_{t+1}$, $A_{t+1}$)을 구한다.

$$\mu(S_{t+1}) = \underset{a}{\text{argmax }} Q(S_{t+1}, a)$$

$$Q_\pi^\prime(S_t,A_t) = Q_\pi(S_t, A_t) + \alpha\{R_t + \gamma Q_\pi(S_{t+1}, A_{t+1}) - Q_\pi(S_t, A_t)\}$$

 

여기서, $\underset{a}{\text{argmax }} Q(S_{t+1}, a)$와 $Q_\pi(S_{t+1}, A_{t+1})$는 동일한 연산이기 때문에,

이를 $Q_\pi^\prime(S_t,A_t) = Q_\pi(S_t, A_t) + \alpha\{R_t + \gamma \underset{a}{\max} Q_\pi(S_{t+1}, a)- Q_\pi(S_t, A_t)\}$로 묶어 한번에 처리할 수 있다.

 

3. 갱신된 $Q^\prime(S_t, A_t)$으로 대상 정책인 탐욕 정책을 개선한다.

$$\mu^\prime(S_t) = \underset{a}{\text{argmax }} Q^\prime(S_t, a)$$

참고로, 위 연산은 1번 구간에서 수행해도 되기 때문에 생략 가능하다.

그리고, $Q$가 있으면 $\mu$를 저장하지 않아도 된다.

---

SARSA와 Q-learning 과정을 추상화하면 다음과 같이 표현할 수 있다.