2024. 2. 2. 13:15ㆍML/DL
신경망이 무엇인지 알기 위해선 신경망의 기원인 퍼셉트론에 대해 집고 넘어가야 한다.
1. 퍼셉트론
퍼셉트론(=perceptron)은 "사람의 뇌 신경세포 뉴런의 동작 과정에 영감을 받아 만든 수학적 모델"로,
"다수의 신호(0/1)를 입력으로 받아 하나의 신호(0/1)를 출력하는 모델"을 의미한다.
(참고로, 여기서 이야기하는 퍼셉트론은 "인공 뉴런" 혹은 "단순 퍼셉트론"을 의미한다.)

위 그림은 2개의 입력 신호를 받은 퍼셉트론이다.
$x_1$과 $x_2$는 입력 선호, $w_1$과 $w_2$는 기중치(=weight)를 뜻한다.
(참고로, 원은 노드(=node) 혹은 뉴런(=neuron), 선은 엣지(=edge)라고 부른다.)
그럼 퍼셉트론이 어떤 방식으로 작동하는지 아래 식을 통해 알아보자.
$$f(x_1, x_2, \cdots, x_n) = \begin{cases} 0, & (\mbox{if } w_1x_1 + w_2x_2 + \cdots + w_nx_n \le \theta) \\ 1, & (\mbox{if }w_1x_1 + w_2x_2 + \cdots + w_nx_n > \theta) \end{cases} \quad - (1)$$
($x_1, x_2, \cdots, x_n$은 입력 신호, $w_1, w_2, \cdots, w_n$은 가중치(=weight), $\theta$는 임계값을 뜻한다.)
이 식을 서술하자면 다음과 같다.
퍼셉트론은 "입력 신호와 가중치를 곱하여 더한 값이 임계값을 넘으면 1을 출력하는 모델"이다.
(참고로, "임계값을 넘어 1을 출력한다"는 "뉴런을 활성화한다"라고도 표현한다.)
1.1. 가중치(=weight)와 편향(=bias)의 의미
퍼셉트론의 수식(1)도 직관적이지만, 더 직관적으로 만들어보기 위해 $\theta$를 -$b$로 치환해 식을 다음과 같이 수정해봤다.
$$f(x_1, x_2, \cdots, x_n) = \begin{cases} 0, & (\mbox{if } b + w_1x_1 + w_2x_2 + \cdots + w_nx_n \le 0) \\ 1, & (\mbox{if } b + w_1x_1 + w_2x_2 + \cdots + w_nx_n > 0) \end{cases} \quad - (2)$$
($x_1, x_2, \cdots, x_n$은 입력 신호, $w_1, w_2, \cdots, w_n$은 가중치(=weight), $b$는 편향(=bias)를 뜻한다.)
여기서 가중치(=weight)는 "입력 신호의 영향력(=중요도)"을 의미하며,
편향(=bias)는 "뉴런의 활성화 난이도"를 의미한다.
다시 말해, 가중치는 "입력 신호가 결과에 주는 영향력(=중요도)을 조절"하는 역할을 하며,
편향은 "뉴런이 얼마나 쉽게 활성화되느냐를 조절"하는 역할을 한다.
(참고로, 가중치와 편향을 매개변수 혹은 파라미터라고 부른다.)
1.2. (단순) 퍼셉트론 예시: AND, OR, NAND 게이트
그럼 지금까지 살펴본 (단순) 퍼셉트론으로 무엇을 할 수 있을까?
(단순) 퍼셉트론으로 (AND, OR, NAND 게이트와 같은) 간단한 모델을 표현(=구현)할 수 있다.
| $x_1$ | $x_2$ | $y_\text{AND}$ | $y_\text{OR}$ | $y_\text{NAND}$ |
| 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 |
위 AND, OR, NAND 진리표를 만족하는 $w_1$, $w_2$, $b$ 조합은 수없이 많지만 임의로 하나를 정해보면 다음과 같다.
| $w_1$ | $w_2$ | $b$ | |
| AND | 1.0 | 1.0 | -1.0 |
| OR | -0.5 | -0.5 | 1.0 |
| NAND | -0.5 | -1.0 | 1.0 |
여기서 중요한 점은 "똑같은 퍼셉트론 구조를 가져도 매개변수의 값이 다르면 다른 모델로 변신할 수 있다"는 것이다.
1.3. (단순) 퍼셉트론의 한계
지금까지, (단순) 퍼셉트론으로 AND, OR, NAND 게이트를 표현할 수 있음을 보였다.
그럼 XOR 게이트도 (단순) 퍼셉트론으로 표현할 수 있을까? 정답부터 말하자면, 못한다!
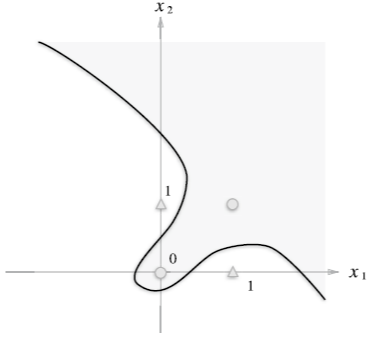
그 이유에 대해 설명하자면, AND, OR, NAND 게이트는 직선으로 표현할 수 있는 선형 모델이라면,
XOR 게이트는 곡선으로 표현할 수 있는 비선형 모델이고, (단순) 퍼셉트론은 선형 모델만 표현할 수 있기 때문이다.

1.4. 다층 퍼셉트론
위에서 설명한 것처럼, (단순) 퍼셉트론으로 (XOR 게이트와 같은) 비선형 모델을 표현할 수 없다.
그렇다고 너무 낙담할 필요는 없다. 왜냐하면, 퍼셉트론을 조합하여 혹은 층을 쌓아 표현할 수 있기 때문이다.
이처럼, 퍼셉트론의 아름다움은 "층을 쌓아 다층 퍼셉트론을 만들 수 있다"는데 있다.
(참고로, 퍼셉트론을 조합하여 혹은 층을 쌓아 만든 것을 다층 퍼셉트론이라고 한다.)

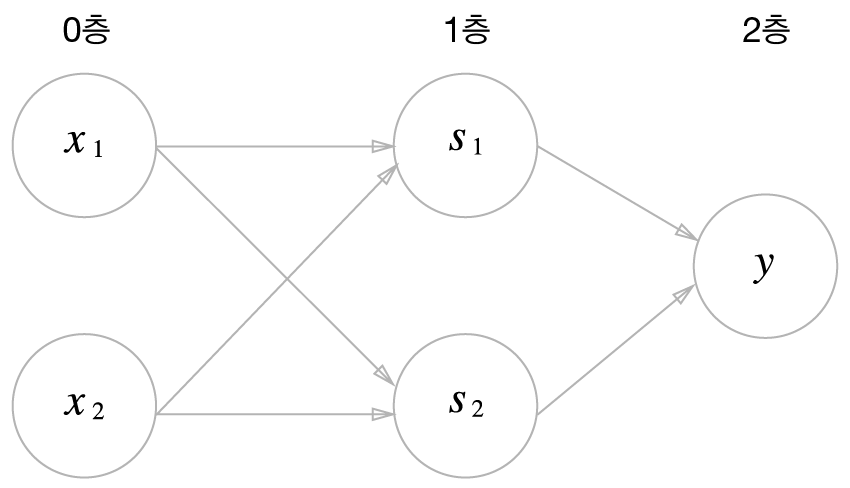
위 그림은 XOR 게이트를 표현한 2층 퍼셉트론이다.
위 2층 퍼셉트론의 동작을 서술하자면:
1). 0층의 두 뉴런이 "입력 신호($x_1, x_2$)"를 1층의 뉴런으로 보낸다.
2). 1층에서 전달 받은 입력 신호로 "중간 신호($s_1, s_2$)"를 만들어 2층의 뉴런으로 보낸다.
3). 2층에서 전달 받은 중간 신호로 "출력 신호($y$)"를 만들어 반환한다.
이때, 우리는 "$x_1, x_2$의 XOR값"을 알기 위해, "$x_1, x_2$의 OR값과 NAND값"을 사용했다.
다시 말해, "입력값의 두 가지 특징(=중간 특징)"으로 "원하는 특징(=출력 특징)"을 얻었다.
1.5. 다층 퍼셉트론의 잠재력 및 설계 방향성
더 나아가, 다층 퍼셉트론은 지금까지 본 회로보다 더 복잡한 회로를 표현할 수 있고, 심지어 컴퓨터까지도 표현할 수 있다.
정확히는, 2층 퍼셉트론으로 모든 연속 함수를 표현할 수 있음이 증명됐다. (by Universal Approximation Theorem)
("노드 2개 당 지점(=데이터, (x, y)) 하나를 표현"할 수 있기 때문이다.)
하지만, 노드 2개 당 지점 하나를 표현해 모든 연속 함수를 표현할 수 있는 것이지, 이러한 방향으로 학습되는 것이 아님을 명심해라!
쉽게 말해, 1층에 무수히 많은 노드가 있어도 "노드 2개 당 지점 하나를 표현"하는 방향으로 학습되지 않는다.
그리고, 2층 퍼셉트론 구조로 컴퓨터를 만들기란 매우 어려운 작업이다.
1). 구조를 적절히 설계하는 것 뿐만이 아니라, 2). 가중치를 적절히 설정하는 것이 매우 어렵기 때문이다.
그뿐만 아니라, 2층 퍼셉트론으로 표현하는 것은 매우 비효율적이다. 층을 늘리면 훨씬 더 적은 노드로 표현이 가능하기 때문이다.
그래서 실제로 컴퓨터를 만들 때 필요한 부품(=모듈 or 중간 특징)을 단계적으로 만들어가는 방식을 사용한다.
예를 들어, AND와 OR 게이트, 그 다음 반가산기와 전가산기, 그 다음에는 산술 논리 연산 장치(ALU), 그 다음에는 CPU 식으로..
이처럼, 퍼셉트론으로 모델(=함수)를 구현할 때, 필요한 모듈(=중간 특징)을 단계적으로 구현하는 방식을 차용해야 한다.
만약, 필요한 모듈이 뭔지 모르겠으면, "필요한 모듈이 무엇일지 대략적으로 추정"하여 구현하면 된다.
이후, 해당 모듈의 매개변수는 입출력 데이터로 찾으면 된다.
(물론, 추정한 모듈은 말 그대로 추정한 것이기 때문에, 모델 구현에 필요할 수도 있고, 필요하지 않을 수도 있다.
만약 필요한 경우, 입출력 관계를 적절히 나타내는 가중치가 존재할 것이다.
하지만 필요하지 않는 경우, 입출력 관계를 적절히 나타내는 가중치는 당연히 존재하지 않을 것이다.
요약하자면, 가중치가 존재하면 필요한 모듈이고, 존재하지 않으면 필요하지 않은 모듈이다.)
1.6. 다층 퍼셉트론의 한계점
그럼 퍼셉트론도 선형 회귀에서 사용한 최적화 기법 gradient descent로 매개변수를 찾을 수 있을까?
정답은 "찾을 수 없다"이다. 왜냐하면, 퍼셉트론 매개변수 미분값은 계단 함수에 의해 0 혹은 불가능이기 때문이다.
직관적으로 설명하자면 다음과 같다.
모든 (단순) 퍼셉트론의 출력값 $y$는 0 또는 1이다.
이는 $w_i$의 순간 변화량에 따른 $y$의 순간 변화량은 고정(0-→0 or 1→1) 혹은 이동(0→1 or 1→0)을 의미한다.
만약 고정이라면, $w_i$의 미분값은 0이고, 이동이면 미분이 불가능하다.
그렇기 때문에, 퍼셉트론은 최적화 기법 중 하나인 gradient descent 기법을 사용할 수 없다.
2. (인공) 신경망
앞에서 살펴본 퍼셉트론은 "임의의 함수를 구현할 수 있다"는 뛰어난 장점이 있지만,
"최적화 기법 gradient descent 기법을 사용할 수 없다"는 치명적인 단점이 존재한다.
(인공) 신경망은 "계단 함수를 말고 다른 비선형 함수를 사용해 이러한 단점을 보완한 퍼셉트론"이다.
이를 수학적으로 표현하면 다음과 같다.
(인공) 신경망은 선형 조합(linear combination)과 미분 가능한 비선형(non-linear) 함수를 반복적으로 쌓아올린 함수다.
(Artificial) Neural Network is function approximators that stack affine transformations followed by non-linear transformations.

위 그림은 2층으로 구성된 (인공) 신경망이다.
(인공) 신경망은 입력층(=input layer), 은닉층(=hidden layer), 출력층(=output layer)으로 구성되어 있다.
그림에서 보았듯이, 신경망과 퍼셉토론의 구조와 작동 원리는 ("활성화 함수"를 제외하면) 동일하다.
2.1. 차이점1: 활성화 함수
(단순) 퍼셉트론의 작동 원리는 수식(2)과 같다.
$$h(x_1, x_2, \cdots, x_n) = \begin{cases} 0, & (\mbox{if } b + w_1x_1 + w_2x_2 + \cdots + w_nx_n \le 0) \\ 1, & (\mbox{if } b + w_1x_1 + w_2x_2 + \cdots + w_nx_n > 0) \end{cases} \quad - (2)$$
이를 다음과 같이 두 단계로 나눠 더 간결하게 작성하면 다음과 같이 표현할 수 있다.
$$a = b + w_1x_1 + w_2x_2 + \cdots + w_nx_n \quad - (3.1) \\ h(a) = \begin{cases} 0 & (\mbox{if } a \le 0) \\ 1, & (\mbox{if } a > 0) \end{cases} \quad - (3.2)$$
여기서 우리는 $h(x)$를 "활성화 함수"라고 부른다.
"가중치가 곱해진 입력 신호의 총합이 뉴런의 활성화를 일으키는지를 정하는 함수"이기 때문이다.
이처럼, 퍼셉트론은 활성화 함수로 계단 함수를 사용한다.
하지만, 신경망은 미분 문제를 해결하기 위해 계단 함수 이외 함수를 활성화 함수(e.g., 시그모이드 함수)로 사용한다.
아래 식은 활성화 함수로 시그모이드 함수를 사용하는 신경망 노드의 작동 원리이다.
$$a = b + w_1x_1 + w_2x_2 + \cdots + w_nx_n \quad - (4.1) \\ h(a) = \frac{1}{1 + e^{(-a)}} \quad - (4.2)$$
참고로, 신경망 노드는 다음과 같이 표현한다.

2.1.1. 계단 함수 vs 시그모이드 함수
계단 함수와 시그모이드 함수의 차이점은 "연속/비연속"이다.

시그모이드 함수는 "$y$값이 연속적인 연속 함수"인 반면, 계단 함수는 "원점에서 갑자기 0→1, 1→0으로 값이 바뀌는 비연속 함수"이다.
공통점에는 세 가지가 있다.
첫번째, 출력값이 0과 1 사이다. 두번째, 입력이 중요하면 큰 값을 출력하고 입력이 중요하지 않으면 작은 값을 출력한다. 세번째, "비선형 함수"다.
여기서 알 수 있듯이, 신경망에서는 활성화 함수는 무조건 비선형 함수를 사용해야 한다.
왜냐하면, 비선형 함수말고 선형 함수를 활성화 함수로 사용하면, 아무리 층을 쌓아도 선형 함수가 돼 비선형 문제를 풀지 못하기 때문이다.
다시 말해, 선형 문제만 풀 수 있고, 이는 1층 (인공) 신경망으로도 풀 수 있어, 층을 쌓는 이유가 없어진다.
2.2. 차이점2: 노드 구조에 자유성 부여
퍼셉트론 노드는 "선형 방정식 + 활성화 함수(=계단 함수)"로 구조가 고정되어 있다.
하지만, (인공) 신경망은 노드 구조에 제약을 두지 없다. 다시 말해, 아무 함수를 사용해도 된다.
(예를 들어, flatten layer, softmax layer)
물론 다층 퍼셉트론(or 신경망)은 모든 함수를 표현할 수 있어, 굳이 자유성 부여를 하지 않아도 된다.
(때문에, (인공) 신경망을 "계단 함수를 활성화 함수로 사용하지 않은 퍼셉트론"으로 소개해도 무리가 없다.)
하지만, 모델을 보다 간결하게 만들 수 있다면 굳이 제약을 둘 필요가 없기에, 노드 구조에 자유성을 부여했다.
2.2.1. (인공) 신경망은 (매개)변수가 없는 노드 (or 레이어)를 허용한다
DL 모델(DNN)을 사용하는 이유는 "문제를 푸는데 유용한 특징을 직접 찾기 어려워서"이다.
다시 말해, 문제를 푸는데 유용한 특징이 무엇인지 모르겠지만,
유용한 특징을 어떤 방식으로 추출해야 할지 (대략적으로) 즉, 함수 형태는 추정할 수 있어 이를 DNN으로 설계한 것이다.
하지만, 문제를 푸는데 유용한 특징을 (구할 수 있는 함수를) 추정할 수 있다면, 이를 노드(or 레이어)로 표현해 사용하는 것이 당연하다.
그렇기 때문에, 매개변수가 없는 노드 (or 레이어)를 허용하는 것은 당연한 것이다.
추가. 인공 신경망 != 인간의 뇌
하늘을 날고 싶다 해서 새처럼 날 필요가 없고, 빠르게 달리고 싶다 해서 치타처럼 달릴 필요가 없다.
이와 마찬가지로, 인간의 지능을 모방하고 싶다 해서 인간의 뇌를 굳이 모방할 필요는 없다.
인공 신경망도 인간의 뇌 신경세포 뉴런의 동작 방식을 모방하는 것으로부터 시작했을지 모르겠지만,
지금의 딥러닝 방식은 인간의 뇌 신경세포 동작 방식과 너무 많이 다르다.
그렇기 때문에, 딥러닝을 설명할 때, 인간의 뇌 신경세포 관점이 아닌 수학적 관점으로 설명하는 것이 더 옳다고 생각한다.
'ML > DL' 카테고리의 다른 글
| [DL] 5.1. Model hyper-parameter: Weight initialization (0) | 2024.02.18 |
|---|---|
| [DL] 4. Backpropagation (0) | 2024.02.13 |
| [DL] 3.1. Advanced Optimization (Momentum, RMSprop, Adam) (0) | 2024.02.13 |
| [DL] 3. Optimization (GD, SGD) (0) | 2024.02.10 |
| [DL] 2. Loss Function (MSE, CEE) (0) | 2024.02.08 |