[DL] 3. Optimization (GD, SGD)

저번 글에서, "손실 함수"가 무엇인지 대해 알아봤다.

그리고, 손실 함수를 활용해 최적의 매개변수를 구하는 무식한(?) 방법 두 가지에 대해서도 살펴봤다.

 

첫번째, 매개변수를 일일이 바꿔가며 손실값이 가장 낮은 매개변수를 찾는다.

위 방식은 시간이 매우 오래 걸리는 매우 무식한 방법이다.

 

두번째, "손실 함수(Loss(($\hat\theta$)의 도함수를 구해 미분값이 0이 되는 부분을 찾는다.

위 방식도 매우 비효율적이다. 왜냐하면, 함수가 복잡해질수록 도함수 구하기가 매우 어려워지기 때문이다.

 

이번 글에서는, 위 방식보다 더 빠르고 효율적이게 최적의 매개변수($\hat\theta$)를 구하는 방법에는 무엇이 있는지 알아볼 것이다.

 

1. 경사 하강법(Gradient Descent)

경사 하강법은 "매개변수의 미분값(=기울기)로 함수의 최솟값 위치를 추정하는 방식"이다.

 

1. 무작위로 매개변수($\theta$)를 선정한다. 

2. 손실($\text{Loss}(\theta)$)을 줄이는 방향을 찾는다.

    2.1. 수치 미분으로 $\text{Loss}(\theta)$에 대한 $\theta$의 미분값(=기울기)$\left({\partial \text{Loss}(\theta) \over \partial \theta}\right)$를 구한다.

    2.2. 기울기가 음수면 양의 방향으로 이동하고, 양수면 음의 방향으로 이동한다.

    다시 말해, 기울기의 반대 방향으로 이동한다. 추가로, 학습률(learning rate, $\gamma$)을 곱해 학습 속도를 조절한다.

$$\theta_{t+1} = \theta_t - \gamma_{\theta_t} {\partial \text{Loss}(\theta_t) \over \partial \theta_t}$$

3. 손실값이 줄어들지 않을 때까지 2번을 반복한다.

 

위와 방식을 사용하면 보다 효율적으로 최적의 매개변수$\hat \theta$를 구할 수 있다.

 

학습률(learning rate)이란?

학습률은 학습 속도를 조절하는 하이퍼 파라미터이다.

학습률을 높이면 빠른 학습 속도를 기대할 수 있지만, loss가 발산하여 학습이 전혀 진행되지 않을 수 있다.

그렇다고 학습률을 낮추면 loss가 발산하는 것을 막을 수 있지만, 학습 속도가 느려질 뿐만 아니라, 이로 인해 쉽게 극솟값에 갇힐 수 있다.

이러한 이유로, 맨 오른쪽 그림(그래프)을 참고하여 적절한 학습률을 찾아야 한다.

학습률 설정 방법에 대해서는 추후 더 자세히 다룰 것이다. 

 

경사 상승법(gradient ascent)

만약, 함수값이 클수록 매개변수가 최적에 가까워지는 함수를 판단 기준으로 사용할 경우, 최솟값 대신 최댓값을 찾는 문제로 바뀐다.

하지만 그렇다고 본질은 달라지지 않았다.

기울기 반대 방향 대신 기울기와 같은 방향으로 매개변수를 이동시켜 최솟값 대신 최댓값을 추정하는 경사 상승법을 사용하여 문제를 풀면 된다.

한계점

1. 부정확한 미분값

위 방식은 수치 미분$\left(\frac{f(x+h) - f(x)}{h}\right)$으로 미분값을 계산하기 때문에, 진정한 미분값이 아니다.

그뿐만 아니라, 컴퓨터는 표현의 한계가 존재하기 때문에, 실제 계산 결과와 차이가 있을 수 있다.

이와 같은 이유로, 실제 미분값과 오차가 약간 발생할 수 있다.

 

물론, 컴퓨터를 사용하는 한, 오차가 존재할 수 밖에 없지만,

이는 다음 글에서 설명할 오차역전파법으로 어느 정도 해소할 수 있다.

 

2. 극솟값(local minimum)

GD의 한계점은 "기울기가 가리키는 방향에 함수의 최솟값이 있는지 보장할 수 없다"는 것이다.

사실 기울기의 반대 방향은 (현 위치에서 함수의 최솟값이 있는 방향이 아니라,) 현 시점에서 손실을 가장 크게 줄이는 방향이다.

---

유도 방법

$$\text{By taylor series, } \text{Loss}(\theta) \simeq \text{Loss} (\theta_t) + (\theta - \theta_t) \left . {\partial \text{Loss} \over \partial \theta^\top} \right|_{\theta=\theta_t} \\ \text{if } \theta_{t+1} = \theta_t + \Delta, \text{then } \text{Loss}(\theta_{t+1}) \simeq \text{Loss}(\theta_t) + \Delta \left . {\partial \text{Loss} \over \partial \theta^\top} \right|_{\theta=\theta_t} \\ \text{Loss}(\theta_{t+1}) - \text{Loss}(\theta_t) \simeq \Delta \left . {\partial \text{Loss} \over \partial \theta^\top} \right|_{\theta=\theta_t}$$

 

loss를 최대한 줄이기 위해서는 $\text{Loss}(\theta_{t+1}) - \text{Loss}(\theta_t)$이 최대한 커야 한다. 

그러기 위해서는, $\Delta$의 방향이 기울기 방향$\left( \left . {\partial \text{Loss} \over \partial \theta^\top} \right|_{\theta=\theta_t} \right)$과 일치해야 한다. (내적 개념)

(이때, $\Delta$의 방향에 대해서만 생각하기 위해 크기는 고정되어 있다고 가정한다.)

---

실제로 기울기가 가리키는 방향에 함수의 최솟값이 있는 경우는 극소수다.

하지만, 위 한계점을 보완한 알고리즘은 아직까지 존재하지 않아, 현재로써 위 방식이 최선이다.

 

추가

위 그림에서 알 수 있듯이, 매개변수가 어디에서 시작하느냐에 따라 도달 위치(최솟값 or 극솟값)가 달라진다.

이처럼, "매개변수의 초깃값을 무엇으로 설정하냐"가 학습의 성공을 좌우하기도 한다.

그렇기 때문에, 매개변수 초기화 방법에 대해서는 차후에 더 자세히 다룰 것이다.

 

3. 느린 학습

위 방식은 데이터 전체를 사용해 미분값을 구하기 때문에 정확한 방향을 구할 수 있다.

하지만, 이는 많은 메모리 사용량과 계산량을 필요로 하기 때문에 학습이 매우 느려진다.

2. 확률적 경사 하강법 (Stochastic Gradient Descent, SGD)

확률적 경사 하강법은 "데이터 하나만으로 매개변수의 미분값(=기울기)을 구해 함수의 최솟값 위치를 추정하는 방식"이다.

(SGD라고 부르는 이유는 확률적 무작위로 데이터 하나만 추출해 경사 하강법으로 매개변수를 갱신하는 기법이기 때문이다.)

 

위 방식은 데이터 한 개만 사용하기 때문에, 기울기 연산이 빨라져 학습이 빨라진다.

물론, 아래 그림처럼 "불필요한 진동(=이동) or 방향 오차가 발생한다"는 단점이 있다.

그렇기에, SGD을 사용할 때는 보다 조심스럽게 학습률을 조작해 불필요한 이동을 줄여야 한다.

 

하지만 문제(손실 함수)가 non-convex일 경우, 이러한 오차는 극솟값 탈출 기회를 제공하기도 한다.

다시 말해, 손실 함수의 그래프 모양이 약간씩 바뀌어 극솟값을 벗어날 기회가 생긴다.

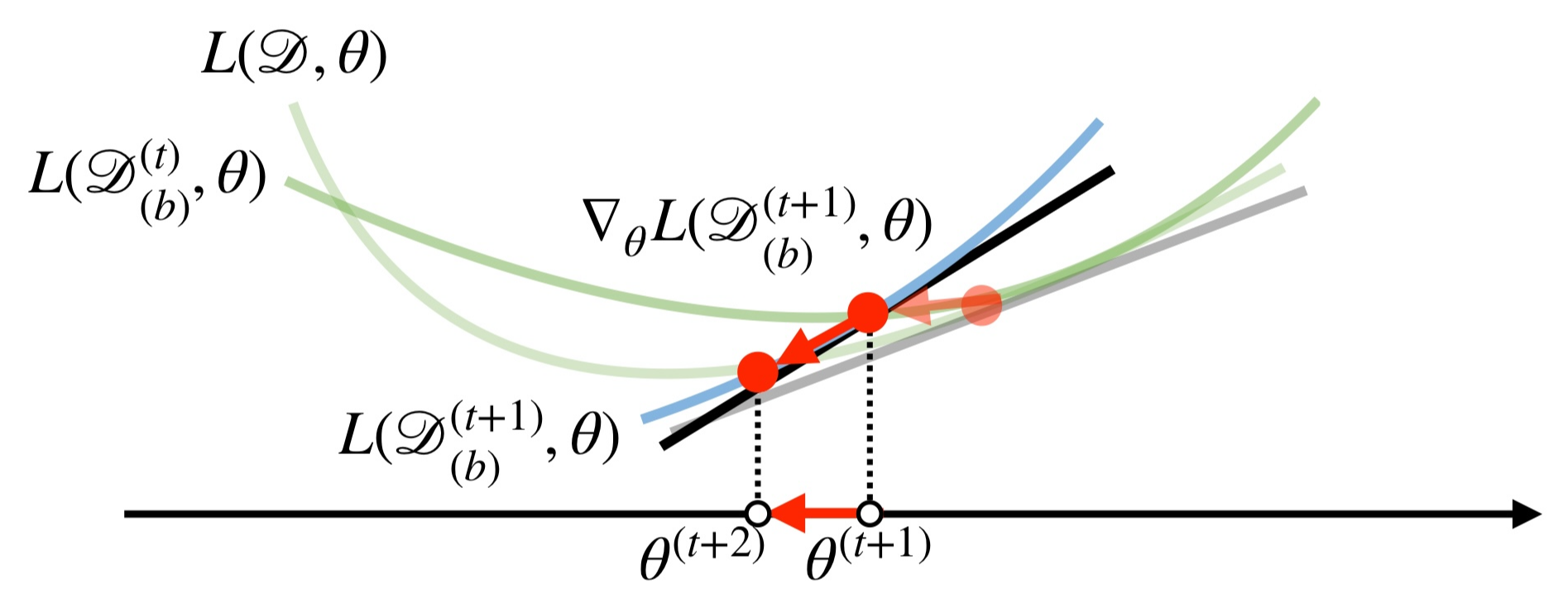
3. mini-batch SGD

GD는 정확한 방향을 구할 수 있지만 너무 느리다. 반면에 SGD는 빠르지만 불필요한 이동이 크다.

두 기법 모두 너무 한쪽으로 치우져 있어 극단적이다.

"미니배치(=mini-batch) 학습"은 두 요소의 균형을 잡아줘 효율적으로 학습하도록 도와준다.

 

미니배치 학습은 데이터의 일부(=batch)만 추출해 학습을 수행하는 방식이다.

데이터 일부로 전체 데이터를 근사하여 매개변수 갱신하기 때문에,

SGD보다 불필요한 이동을 줄일 수 있고 GD보다 빠른 학습 속도를 가진다.

 

그래서 GD, SGD를 단독으로 사용하지 않고, 미니배치 학습과 같이 사용한다. 이를 "mini-batch SGD"라고 한다.

---

다음 글에서는 수치 미분보다 빠르게 미분값을 계산하는 방법(backpropagation)에 대해 알아볼 것이다.

이는 학습 속도를 훨씬 빠르게 높여 위 한계점을 더욱 보완해줄 것이다.