2024. 2. 13. 14:24ㆍML/DL
저번 글에서는, 기본적인 최적화 기법인 GD와 SGD에 대해 살펴봤다.
그 두 가지 기법 모두 수치 미분으로 미분값을 계산했다.
수치 미분은 구현하기 쉽지만, 계산 시간이 오래 걸린다는 단점이 존재한다.
이번 글에서는, 수치 미분보다 효율적으로 미분값을 계산하는 "오차역전파법(backpropagation)"에 대해 살펴볼 것이다.
1. 계산 그래프(computational graph)
계산 그래프는 계산 과정을 그래프로 나타낸 것이다. 노드에는 연산 정보를, 엣지에는 계산 결과를 표기한다.
(이전 글을 통해 눈치채겠지만, 신경망도 대부분 계산 그래프로 표현한다.)
이해를 돕기 위해 간단한 예시 문제의 계산 과정을 어떻게 계산 그래프로 나타낼 수 있는지 살펴보자!
예시 문제1: 슈퍼에서 사과를 2개, 귤을 3개 샀다. 사과는 1개에 100원, 귤은 1개에 150원이며, 소비세는 10%다.
이때, 현빈 군이 지불해야할 총금액의 계산 과정을 계산 그래프로 표현해보자.

계산 그래프는 위와 같이 표현할 수 있으며, 총금액은 왼쪽에서 오른쪽으로 계산을 진행하여 얻을 수 있다.
이처럼, 하류(=입력 방향)에서 상류(=출력 방향)로 전류(=계산값)가 흐르는(=전달되는 or 이동하는) 것을 "순전파(forward propagation)"라고 부른다. (하류에서 전달된 "계산 결과"가 현 노드의 연산(=국소적 계산)을 거쳐 상류로 전달된다.)
반대로, 상류(=출력 방향)에서 하류(=입력 방향)로 전류(=계산값)가 흐르는(=전달되는 or 이동하는) 것을 "역전파(backward propagation)"라고 부른다. (상류에서 전달된 "계산 결과"가 현 노드의 연산(=국소적 계산)을 거쳐 하류로 전달된다.)
계산 그래프는 그래프의 한 종류로 특정 노드에서 계산된 결과를 인접 노드에 쉽고 빠르게 전달할 수 있다는 특징을 가지고 있다. 이러한 특징 덕분에 순전파와 역전파 과정이 매우 쉽고 자연스럽게 진행될 수 있는 것이다.
계산 그래프의 특징
1. 국소적 계산: 아무리 복잡한 계산 과정도 표현할 수 있는 계산 그래프는 국소적 계산을 하는 노드로 구성되어 있다.
다시 말해, 계산 그래프는 "노드의 국소적 계산 결과를 단계적으로 전달"하면 어떠한 복잡한 계산도 풀 수 있다.
2. 중간 계산 결과 저장: 계산 그래프는 엣지의 중간 계산 결과를 저장할 수 있다.
3. 역전파: 계산 그래프는 순전파의 반대 방향으로 전류가 흐를 수 있다.
계산 그래프는 위와 같은 특징들 덕분에 "미분"을 효율적으로 계산할 수 있다.
2. 연쇄 법칙(chain rule)
계산 그래프는 역전파 특징 덕분에, 다음과 같이 "연쇄법칙" 원리$\left( {\partial L \over \partial x}={\partial L \over \partial y}{\partial y \over \partial x} \right)$로 미분값을 계산할 수 있다.

위 그림과 같이, 상류에서 최종 결과($L$)에 대한 $y$의 미분값$\left( \partial L \over \partial y \right)$을 전달하면, 현 노드에서 국소적 미분$\left( \partial y \over \partial x \right)$을 하고 이를 $\partial L \over \partial y$와 곱하여 하류에 전달하는 방식으로 최종 결과($L$)에 대한 $x$의 미분값$\left( {\partial L \over \partial x} \right)$을 구할 수 있다. 즉, 연쇄법칙 원리$\left( {\partial L \over \partial y}{\partial y \over \partial x} \right)$로 미분값$\left( {\partial L \over \partial x} \right)$을 구할 수 있다.
뿐만 아니라, 계산 그래프는 중간 결과($y$와 $\partial L \over \partial y$)를 저장 및 공유할 수 있고,
계산 그래프의 각 노드는 국소적 계산($f$)으로 구성되어 있기 때문에, 각 노드의 도함수($f^\prime$)를 수월하게 찾을 수 있어,
보다 효율적으로 미분값을 계산할 수 있다!!
다시 예시 문제로 돌아와, 연쇄 법칙 계산을 계산 그래프의 역전파로 표현해 모든 변수의 미분값을 계산해보자!

위 그래프처럼, 상류에서 전달된 미분값과 현 노드의 국소적 미분값을 곱하고 전달하여 모든 변수의 미분값을 계산할 수 있다.
예시: Sigmoid 함수
sigmoid 함수$\left( y = {1 \over 1 + \exp(-x)} \right)$의 계산 그래프의 역전파를 나타내보자!
우선, sigmoid 함수의 순전파는 다음과 같다.

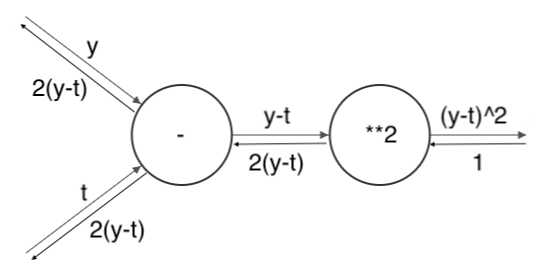
이를 기반으로 역전파를 표현하면 다음과 같다.

이때, 역전파 결과$\left( {\partial L \over \partial y} y^2 \exp(-x) \right)$는 순전파의 입출력($x, y$)만으로 계산할 수 있음을 알 수 있다.
그래서, 이 계산 그래프의 중간 과정을 모두 묶어 단일 "sigmoid" 노드로 대체할 수 있다.

이처럼, 계산 그래프를 간소화하면 중간 계산들을 생략하여 더 효율적인 계산할 수 있다.
여기서 더 나아가, ${\partial L \over \partial y} y^2 \exp(-x)$는 더 간단하게 ${\partial L \over \partial y} y(1-y)$로 표현할 수 있다.
이로 인해, 순전파의 출력($y$)만으로 역전파를 계산할 수 있게 되어, 역전파를 위한 정보를 최소화할 수 있게 되었다.

2. 오차역전파법(Backpropagation)
분류 문제일 경우 대부분 출력층으로 "softmax 함수"를, 손실 함수로 "cross entropy error"를 사용한다.
그리고, 회귀 문제일 경우 대부분 출력층으로 "항등 함수"를, 손실 함수로 "mean square error"를 사용한다.
왜냐하면, 두 경우 모두 역전파(=미분값으)로 $y_i - t_i$라는 결과를 내놓기 때문이다.
(참고로, $y_i$는 예측값, $t_i$는 정답을 의미한다.)

학습 목표는 "예측값(=신경망의 출력값)이 정답과 가장 가까워지도록 매개변수의 값을 조정"하는 것이다.
그래서 "예측값과 정답의 오차 정보"를 효율적(?)으로 하류쪽에 전달해야 한다.
그래야 오차가 클 때 보완할 부분이 커 학습 정도가 커지고, 오차가 작을 때는 보완할 부분이 적어 학습 정도가 작아지기 때문이다.
근데, 위 두 경우는 "예측값과 정답의 오차 그 자체"($y_i - t_i$)를 미분값으로 제공하기 때문에 학습에 매우 효과적이다.
기울기 검증
지금까지 기울기를 구하는 방법을 두 가지 대해 설명했다.
하나는 수치 미분을 사용하는 방법, 또 하나는 오차역전파법(=연쇄법칙)으로 해석적 미분을 하는 방법
후자인 해석적 미분은 오차역전파법을 사용해 보다 빠르게 미분값을 계산할 수 있다.
그러니 지금부터 학습 때 느린 수치 미분 대신 오차역전파법을 사용할 것이다.
그럼 수치 미분은 더 이상 필요 없는 것인가? 아니다. 수치 미분은 학습 전 역전파가 정확히 구현했는지를 확인할 때 사용할 것이다.
수치 미분의 이점은 구현하기 쉽다는 것이다. 반대로, 오차역전파법은 구현하기 복잡하다.
그래서, 수치 미분으로 오차역전파법을 제대로 구현했는지 검증해야 한다.
이처럼, 두 방식으로 구한 기울기가 일치함을 확인하는 작업을 "기울기 확인(gradient check)"라고 한다.
(참고로, 컴퓨터는 표현의 한계가 존재하기 때문에, 올바르게 구현했더라도
수치 미분과 오차역전파법의 오차가 0이 되는 경우는 매우 드물 것이며, 대부분 0에 아주 가까운 값이 될 것이다.)
'ML > DL' 카테고리의 다른 글
| [DL] 5.2. Optimizer hyper-parameter: batch size & learning rate (0) | 2024.02.27 |
|---|---|
| [DL] 5.1. Model hyper-parameter: Weight initialization (0) | 2024.02.18 |
| [DL] 3.1. Advanced Optimization (Momentum, RMSprop, Adam) (0) | 2024.02.13 |
| [DL] 3. Optimization (GD, SGD) (0) | 2024.02.10 |
| [DL] 2. Loss Function (MSE, CEE) (0) | 2024.02.08 |